Équation différentielle :  avec e = 1 pour la roulette elliptique (ellipse de demi-axes a et b (a > b)),  e = –1 pour la roulette hyperbolique (hyperbole de demi-axes a et b). Equation cartésienne : . Paramétrisation cartésienne dans le cas elliptique :  où , e = c / a . Abscisse curviligne : . Paramétrisation cartésienne dans le cas hyperbolique : .

On appelle roulette de Sturm le lieu du centre d'une conique à centre roulant sans glisser sur une droite ; on la désigne par roulette elliptique ou hyperbolique suivant que la conique est une ellipse, ou une hyperbole.
 
 

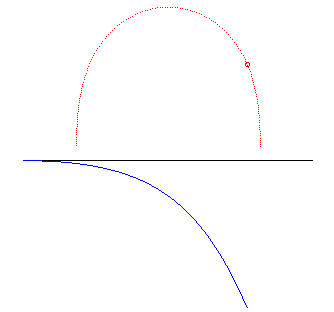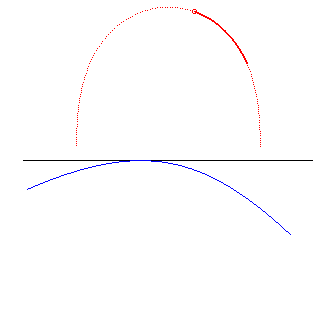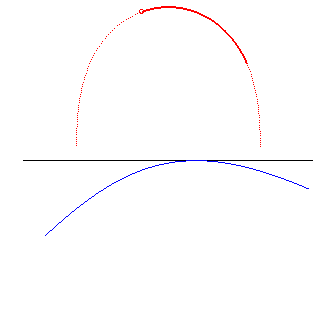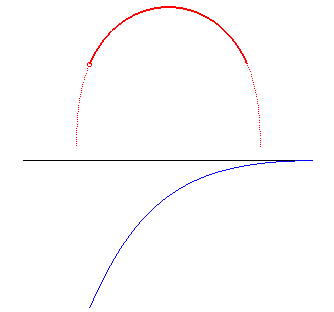
A grand axe constant, dans le cas elliptique, la roulette de Sturm passe de la droite (cas du cercle roulant, e = 0), à une réunion de demi-cercles (cas d'un segment "roulant", e = 1).

 

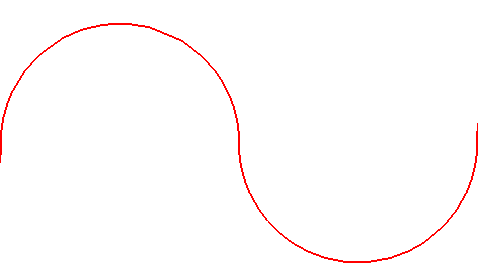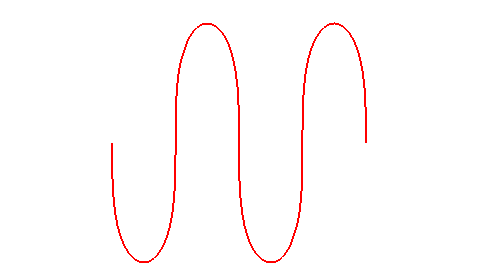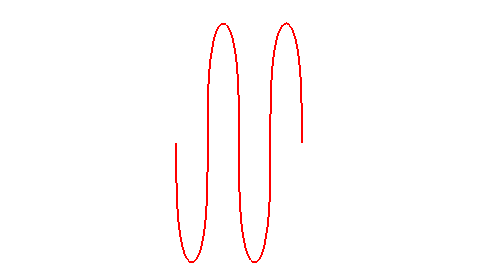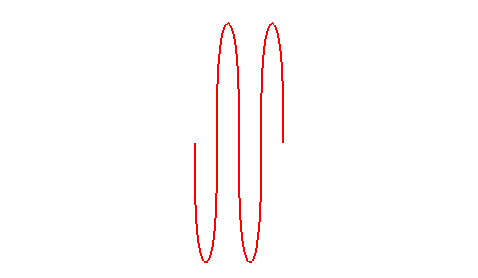A grand axe constant, dans le cas hyperbolique, la roulette de Sturm passe de la réunion de demi-cercles (e = 1) à un segment (e infini).

Le cas particulier d'une hyperbole équilatère () donne la roulette de Sturm équilatère, qui est aussi une lintéaire, ainsi qu'une courbe de Ribaucour (cf. animation de droite en haut de la page).

Voir aussi les roulettes de Delaunay, lieu d'un foyer de la conique, et plus généralement, les roulettes d'ellipse, ainsi que la détermination de la route associée à une roue elliptique.
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2012