Du grec Kissos : lierre.

 

Équation polaire : . Équation cartésienne : . Cubique circulaire rationnelle à point de rebroussement. Paramétrisation cartésienne rationnelle : . Coordonnées du point d'intersection avec l'asymptote : . Coordonnées du point d'abscisse maximale : .

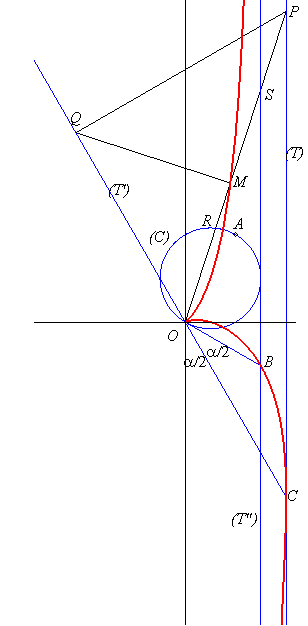
La construction la plus simple d'une cissoïde se fait par double projection : étant donné deux droites (T) et (T') et un point O de (T'), un point variable P de (T) se projette en Q sur (T'), lequel se projette en M sur (OP) : la cissoïde est le lieu de M (voir figure ci-dessus) ; la cissoïde droite est obtenue lorsque (T) et (T') sont strictement parallèles .
Ici, (T) est la droite verticale : x = a, (T') est la droite , faisant un angle  avec la précédente.

Mais la construction classique de la cissoïde est... cissoïdale : étant donné un cercle (C), un point O de ce cercle et une tangente (T") à ce cercle,  un point variable S de (T") est tel que la droite (OS) coupe (C) en R : la cissoïde est le lieu de M tel que.

Les cissoïdes sont donc les cissoïdales de pôle O d'un cercle  (C') passant par O et de la symétrique (T') par rapport à O d'une tangente au cercle (C'); ici, (C') est le symétrique de (C) par rapport à O, d'équation polaire :  et (T") : .
 

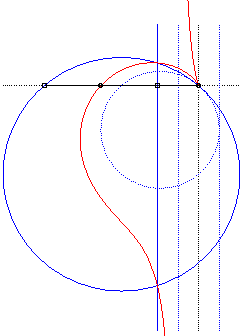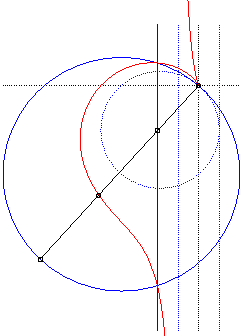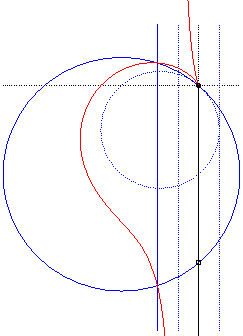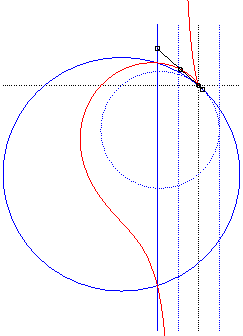Ici, le cercle (C') est le cercle pointillé, le cercle plein étant son homothétique de centre O et de rapport 2, et la droite (T) la droite pointillée de gauche, la droite pleine étant son homothétique de centre O et de rapport 2 ; la cissoïdale est alors la médiane de centre O de ce cercle et de cette droite.

Les cissoïdes peuvent être définies algébriquement comme les cubiques circulaires cuspidales (i.e. ayant un point de rebroussement).
Comme toute cubique circulaire rationnelle, la cissoïde peut être aussi définie comme :
     - podaire d’une parabole par rapport à l'un de ses points (ici la parabole de foyer A et de tangente au sommet  ).

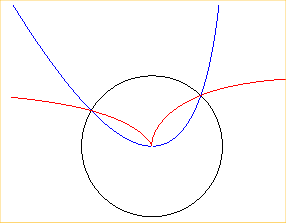
 - inverse d’une parabole par rapport à l'un de ses points (ici la parabole  , le cercle d'inversion étant le cercle (O, a)).

© Robert FERRÉOL 2000