Curve studied by Blaschke in 1908 [Mh. Math. Phys. 19, p. 194] See also [Loria 3d] p. 160.

 

Cartesian parametrization:  traced on the hyperboloid , with . When , , we get the line x = a, by = az. Polar equation of the projection on xOy: .

Here, we consider the helix of the one-sheeted hyperboloid of revolution with vertical axis, a curve with constant slope  with respect to a horizontal plane.
 

View of the 3 kinds of helices:   - in red for a slope < b/a, the helix goes to infinity   - in blue, the line with slope b/a.   - in green for a slope > b/a; the curve has a form of bound (its projection on xOy cannot cross the circle with radius ).

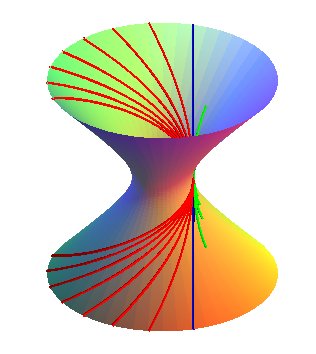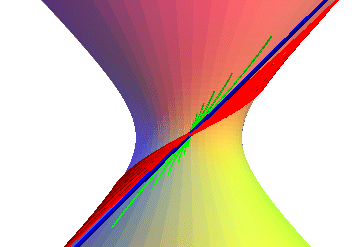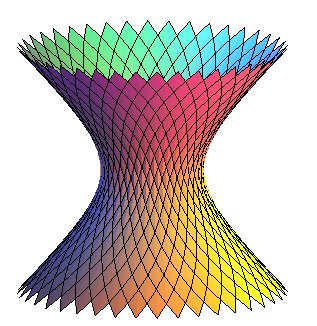
Be careful, if the cylindrical helix is indeed the intersection between a right helicoid and a cylinder, this method does not yield the helix of the one-sheeted hyperboloid, but the following curve, that does not have a name:

Intersection between the helicoid  and the hyperboloid . Cartesian parametrization: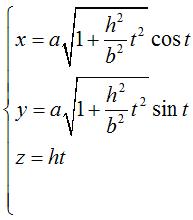; the figure opposite was traced thanks to the parametrization  for which the coordinate lines are the curves under examination here.
Lift on the hyperboloid of the spiral , which is asymptotic to the Archimedean spiral .

 

View of the construction of these curves (by Robert March).

...made by Alain Esculier.

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2018