Feston de toupie

FESTON DE TOUPIE
Spinning top festoon, Kreiselgirlande

Mouvement étudié par Lagrange en 1788, et Poisson en 1809.
Autre nom : courbe du gyroscope.
Voir : Paul Appell : cours de mécanique rationnelle, tome 2, pages 195 à 211

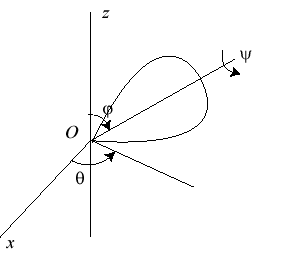
Système différentiel du second ordre obtenu par le théorème du moment cinétique : (le cas kw = 0 donne la courbe du pendule sphérique).
est la longitude, appelée ici la précession, mesurant la rotation autour de Oz.
est la colatitude, appelée ici la nutation, mesurant l'obliquité de la toupie.
est la valeur constante de où est la vitesse de rotation de la toupie (assimilable à dans le cas d'une vitesse grande).
k = J / I où J est le moment d'inertie de la toupie par rapport à son axe et I le moment d'inertie par rapport une droite perpendiculaire à l'axe passant par le point de contact O.
= mga/I où m est la masse de la toupie et a la distance du point de contact au centre de gravité de la toupie.
Intégrales premières :
soit, en posant :
, où , d'où l'
Equation différentielle de la courbe : , .

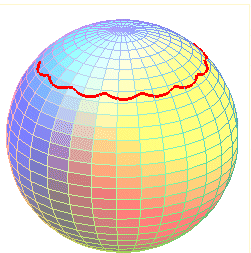
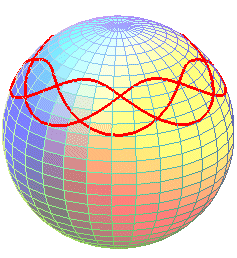
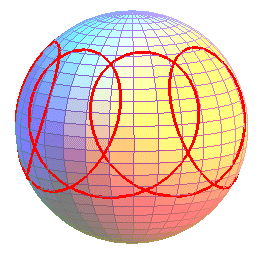
Le feston de toupie est la courbe sphérique décrite par un point de l'axe de révolution d'une toupie (ou d'un gyroscope) en rotation autour de sa pointe, supposée fixe au cours du temps.

Le cas limite d'une toupie à moment d'inertie nul ou qui ne tourne pas donne la courbe du pendule sphérique.

On obtient des courbes ayant la forme de trochoïdes courbées, formées d'une suite d'ondulations ou d'arches joignant alternativement deux parallèles (obtenus pour les valeurs où le polynôme P ci-dessus s'annule). Le cas des arches, similaires à celles des cycloïdes sphériques, est obtenu lors d'une vitesse initiale nulle.

Feston à deux arches (Alain Esculier)

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres