Spinning top festoon

SPINNING TOP FESTOON

Movement studied by Lagrange in 1788 and Poisson in 1809.
Other name: gyroscope curve.
See: Paul Appell : cours de mecanique rationnelle, tome 2, pages 195 to 211

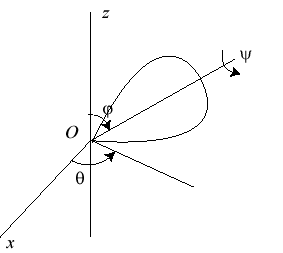
System of differential equations of the second order obtained by considering the angular momentum: (the case kw = 0 gives the curve of the spherical pendulum).
is the longitude, called precession, and measures the rotation around Oz.
is the colatitude, called nutation, and measures the obliqueness of the spinning top.
is the constant value of where is the rotation speed of the top (that can be taken equal to for high velocities).
k = J / I where J is the moment of inertia of the top with respect to its axis and I the moment of inertia with respect to a line perpendicular to the axis passing through the contact point O.
= mga/I where m is the mass of the top and a the distance between the contact point and the center of gravity of the top.
First integrals:
hence, writing :
, where , hence the
Differential equation of the curve: , .

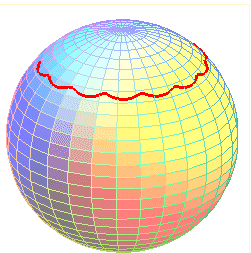
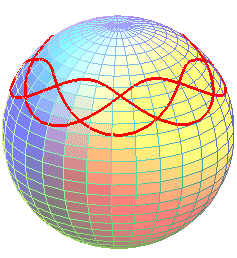
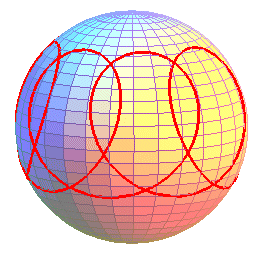
The festoon of a spinning top is the spherical curve described by a point on the axis of revolution of a top (or a gyroscope) rotating around its tip, which is supposed to remain immobile throughout time.

The limit case of a spinning top with zero moment of inertia or that does not spin gives the curve of the spherical pendulum.

We get curves that are similar to curved trochoids, composed of a sequence of undulations or arches joining alternatively two parallel curves (obtained for the values for which the above polynomial P cancels). The case of the arches, similar to that of the spherical cycloids, is obtained when the initial speed is zero.

Festoon with two arches (Alain Esculier)

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra