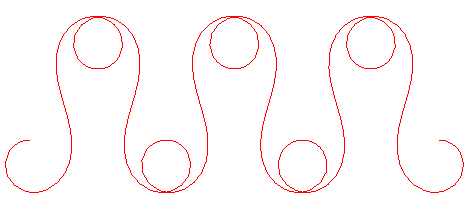
MEANDER CURVE
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
MEANDER CURVE
| Curve studied by Luna Léopold and Walter Langbein
in 1966 (cf. this
article), that they named sine-generated curve.
This curve is also found under the name patterned curve, in this study by Rovenski. |
Intrinsic equation
2: .
Intrinsic equation 1:  .
Cartesian parametrization:  ( );
complex parametrization:  .
Transcendental curve. Remark: the curve parametrized by 
is similar to the previous one. |
The meander curve is the curve such that the angle
formed by the tangent and a fixed direction is a sinusoidal function of
the curvilinear abscissa. Such a curve was considered by Luna Léopold
because he had noticed in an experiment that a compass needle on a boat
sailing at constant speed down a river with meanders oscillated in a sinusoidal
way over time.
In view of the intrinsic equation 1 above, the meander
curve also is the curve for which the curvature varies as a sinusoidal
function of the curvilinear abscissa.
| The meander curve is also the curve described by a point M such that if the angle formed by a line (D) and the tangent at M is proportional to the curvilinear abscissa, then the distance between the projection H of the centre of curvature I on (D) and M is a constant non zero. |  |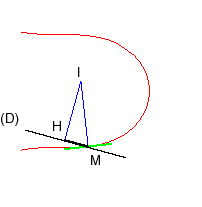
 |
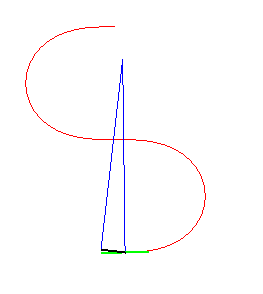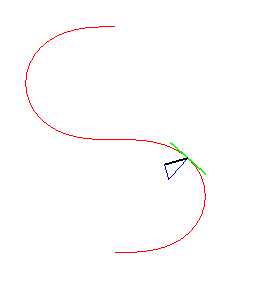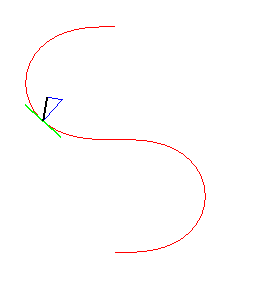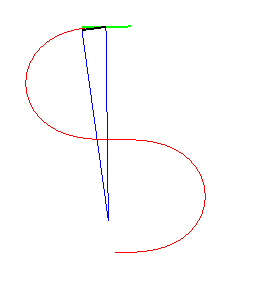Here is the evolution of the curve according to the values
of the maximal tangential angle 
:
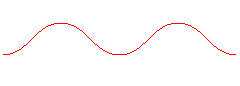 When |
|
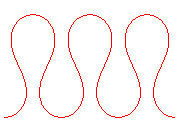
It is when 
that the curve looks the most like meanders. |
|
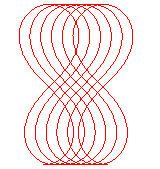
Look when |
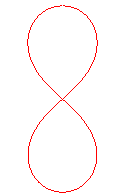
When  ,
the curve looks like a lemniscate |
|
 |
 |
 |
 |
 |
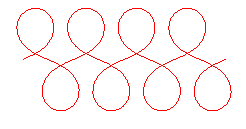
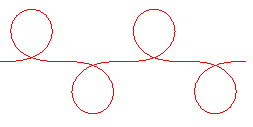
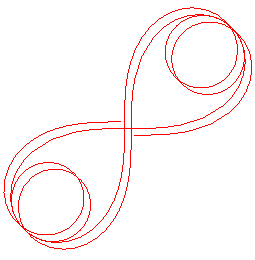
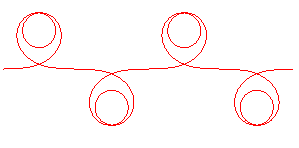
REMARK: the values of
for which the curve is bounded are defined by 
(which implies 
).
When
goes to infinity, the meander curve 
(in red) "goes" to the clothoid: 
(in blue), here when =
10: |
   |
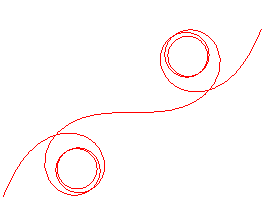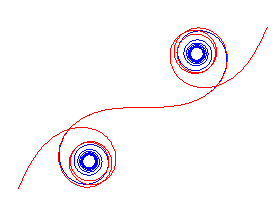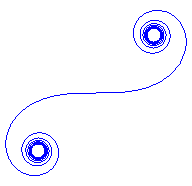Conversely, for small values of ,
the meander curve is very close to the elastic
curve (and this is explained on the corresponding page); in fact, the
interpretation of the meanders as the curve minimising the curvature leads
to modelling meanders rather by the elastic curve, but the comparison between
the two curves shows that Luna Léopold had indeed conducted a good
experimental observation.
Compare also with the curve of
constant gyration and the curves with
sinusoidal radius.
 |
The meanders of the Seine. |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017
,
the curve has a sinusoidal shape; above, 
.
,
