En prenant Oy comme verticale descendante, la conservation de l'énergie donne , et la condition du problème s'écrit , d'où l'équation différentielle de la courbe : . Dans le cas particulier où , cette équation se simplifie en , qui donne comme équation polaire :  pour , avec . Équations horaires du mouvement : . Paramétrisation polaire : , qui donne en utilisant les fonctions elliptiques de Jacobi : .

Une courbe isochrone paracentrique est une courbe telle que si une particule descend par gravité le long d'elle, la distance de la particule à un point fixe O est proportionnelle au temps, le champ de pesanteur étant supposé uniforme ; autrement dit, la particule s'éloigne (ou s'approche) de O à vitesse constante.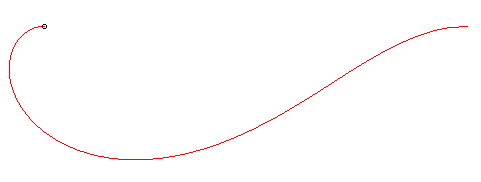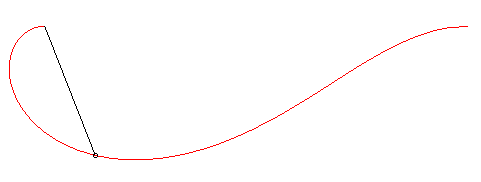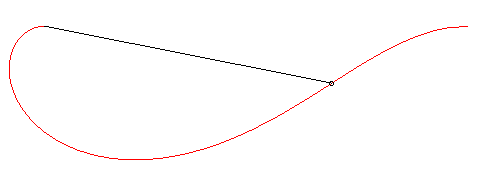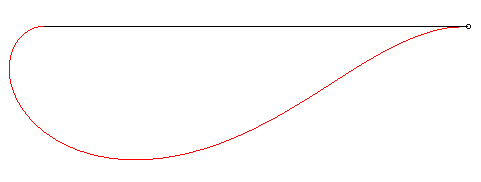

Lorsque la particule descend le long de la courbe rouge, la longueur du segment noir augmente à vitesse constante.

Ci-dessus n'a été résolu qu'un cas particulier () ; dans les autres cas la courbe est en spirale autour de O.
 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2004