Paracentric curve

PARACENTRIC CURVE

Problem posed by Leibniz in 1689 and solved by Jacques Bernoulli in 1694.

With Oy as the descending vertical axis, the conservation of energy gives

, and the condition associated to the problem can be written

, hence the differential equation of the curve:

.
In the special case where

, this equation simplifies to

, which gives the following polar equation:

for

, with

.
Kinematic equations of motion:

.
Polar parametrization:

, which gives, using the elliptic functions of Jacobi,

A paracentric curve is a curve such that if a particle descends along it by the pull of gravity, the distance between the particle and a fixed point O is proportional to time, when the gravitational field is supposed to be uniform; in other words, the particle moves away from (or comes closer to) O at constant speed.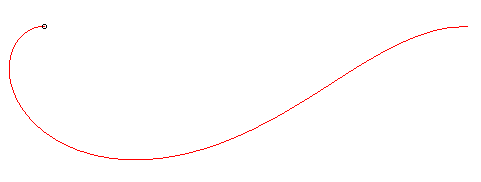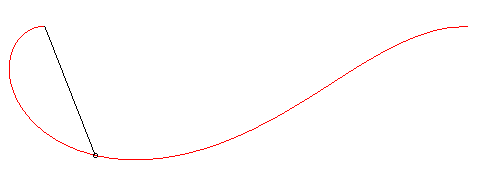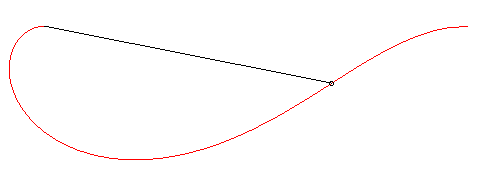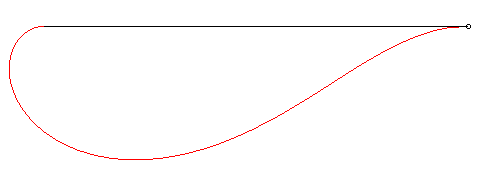

When the particle descends along the red curve, the length of the black segment line increases at constant speed.

Only a special case was solved above; in the other cases, the curve is a spiral around O.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra