| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
CARTÉSIENNE
Cartesian
curve, Kartesische Kurve
| René Descartes (1596-1650) : philosophe, mathématicien et physicien français. |
Équation cartésienne réduite :  .
Si  ,
l'équation prend la forme :
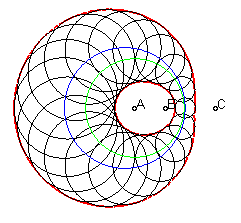
et une définition cyclique a pour cercle déférent
le cercle de centre O et de rayon R,
Dans le repère (A, |
Les cartésiennes sont les quartiques
bicirculaires ayant deux points de rebroussement à l'infini.
Ce sont les courbes ayant une définition cyclique
dont la déférente est un cercle (appelé cercle déférent)
; ce sont, autrement dit, les enveloppes de cercles dont le centre décrit
le cercle déférent, et tels qu'un point fixe ait une puissance
constante par rapport à ces cercles.
Lorsque p < 0, on obtient les ovales
de Descartes complets véritables (???).
, 
=
rayon du cercle directeur :
),
la courbe n'a pas de point réel.
ou
et 
) on
obtient de nouveau (et deux fois) les ovales de Descartes complets véritables.
),
on obtient les cartésiennes dites spéciales, qui ont
une équation tripolaire : 
avec ?? ; ces courbes sont des inverses d'ovales de Descartes.
, 
ou r = 0), on obtient un limaçon
de Pascal.
En résumé, la famille des cartésiennes
est constituée des ovales de Descartes complets et de leurs inverses.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2000
,
et pour puissance d'inversion p.
, 
) :
.
.