Multiellipse

ELLIPSE MULTIFOCALE
Multifocal ellipse (or egglipse), multifokale Ellipse (oder Tschirnhaus'sche Eikurve)

Courbe étudiée par Tschirnhaus en 1686, Maxwell en 1846.
Autres noms : multiellipse, polyellipse, hyperellipse, oeuf de Tschirnhaus.
Sites :
wkipedia anglais (N-ellipses)
wikipedia anglais (Generalized conic)
wikipedia français (point de Fermat-Weber)
http://www.aimath.org/WWN/convexalggeom/AIM.pdf
On the Approximation of Convex, Closed Plane Curves by Multifocal Ellipses
Texte de Maxwell
Article sur le côté algébrique
Sur les triellipses
http://www.journaloftheoretics.com/Articles/6-6/MFCC.pdf?q=foci
Sur le point de Fermat
Gyula Sz.-Nagy (June 1950). "Tschirnhaus'sche Eiflachen und EiKurven". Acta Mathematica Academiae Scientiarum Hungarica 1 (2): 167–181.

Les ellipses multifocales, à n foyers, sont les lieux des points du plan dont la somme des distances à n points est constante.
Equation multipolaire : .
Le cas n = 1 donne bien sûr les cercles.
Le cas n = 2 donne les ellipses classiques. Plus précisément, vaut au minimum AB et pour , donne l'ellipse de foyers A et B et de grand axe a, réduite au segment [AB] pour a =AB.

Pour n = 3, la valeur minimale de est atteinte en un point unique F, appelé point de Fermat du triangle ABC, et les ellipses à trois foyers, appelées triellipses, forment des ovales concentriques autour de F.
Si les angles du triangle sont aigus, le point de Fermat est défini par le fait que l'on y voit les côtés sous des angles de 120° (exemple ci-contre).
Si l'un des angles est supérieur ou égal à 120° le point de Fermat est le sommet correspondant ; dans le cas aplati mais avec des sommets distincts, le point de Fermat est le sommet central. Si deux points sont confondus, le point de Fermat y est situé, et on obtient un ovale de Descartes.
La valeur minimale de la somme vaut où , et a,b,c sont les côtés du triangle.
Comme on le voit ci-contre, les triellipses ont une tangente en tout point sauf lorsqu'elles passent par les sommets du triangle.

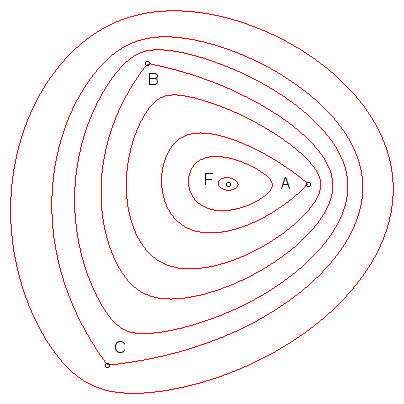Généralisation du tracé du jardinier des ellipses pour le tracé d'une triellipse, proposé par Maxwell.

Ci-contre, le cas d'un triangle équilatéral.

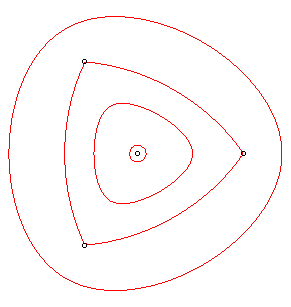Le produit des huit termes étant un polynôme en , la courbe d'équation = 0 (dénommée courbe de Helton-Vinnikov) est algébrique de degré 8, et contient la triellipse .
Par exemple, la courbe algébrique correspondant à la triellipse passant par les sommets du triangle équilatéral précédent, représentée ci-contre, a pour équation :
1331+2628*x^2*y^2+1314*x^4+1314*y^4+512*x^3-124*x^6-372*x^2*y^4-124*y^6+12*x^2*y^6+
12*x^6*y^2+3*y^8+3*x^8-1536*x*y^2-372*x^4*y^2+18*x^4*y^4-3036*x^2-3036*y^2=0
La triellipse n'est constituée que du triangle central rouge ; les trois courbes bleues, vertes et jaunes correspondent aux équations avec deux signes plus (les quatre autres n'ont pas de points réels).
Dans les autres cas, la triellipse n'est qu'une composante connexe ovale de la courbe algébrique en comportant quatre au maximum.

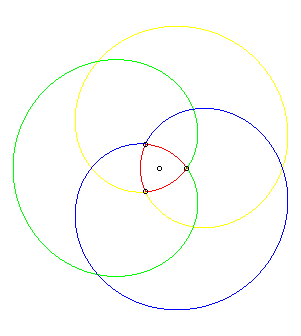Comme pour l'ellipse, la tangente à la triellipse se construit orthogonalement au vecteur .

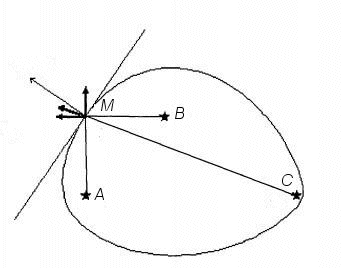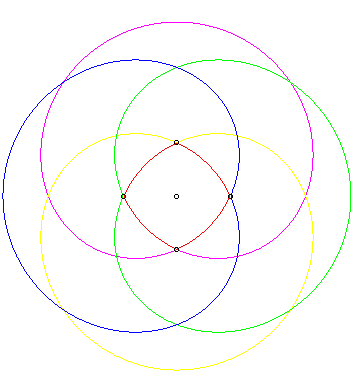
Pour , la somme minimale est toujours obtenue en un point unique, appelé point de Fermat-Weber.
La n-ellipse est incluse dans une courbe algébrique de degré , pouvant être abaissé à quand n est pair.
Ci-contre, la quadriellipse passant par les sommets d'un carré, et la courbe algébrique associée, de degré 16 – 6 = 10.

Comparer avec les cassiniennes, d'équation .

Animation de la triellipse complète associée à un triangle équilatéral, partant de a = 0.
Pour a grand, la courbe tend à devenir un cercle centré au barycentre de .

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres

Pour n = 3, la valeur minimale de est atteinte en un point unique F, appelé point de Fermat du triangle ABC, et les ellipses à trois foyers, appelées triellipses, forment des ovales concentriques autour de F. Si les angles du triangle sont aigus, le point de Fermat est défini par le fait que l'on y voit les côtés sous des angles de 120° (exemple ci-contre). Si l'un des angles est supérieur ou égal à 120° le point de Fermat est le sommet correspondant ; dans le cas aplati mais avec des sommets distincts, le point de Fermat est le sommet central. Si deux points sont confondus, le point de Fermat y est situé, et on obtient un ovale de Descartes. La valeur minimale de la somme vaut où , et a,b,c sont les côtés du triangle. Comme on le voit ci-contre, les triellipses ont une tangente en tout point sauf lorsqu'elles passent par les sommets du triangle.
Généralisation du tracé du jardinier des ellipses pour le tracé d'une triellipse, proposé par Maxwell.
Ci-contre, le cas d'un triangle équilatéral.
Le produit des huit termes étant un polynôme en , la courbe d'équation = 0 (dénommée courbe de Helton-Vinnikov) est algébrique de degré 8, et contient la triellipse . Par exemple, la courbe algébrique correspondant à la triellipse passant par les sommets du triangle équilatéral précédent, représentée ci-contre, a pour équation : 1331+2628x^2y^2+1314x^4+1314y^4+512x^3-124x^6-372x^2y^4-124y^6+12x^2y^6+ 12x^6y^2+3y^8+3x^8-1536xy^2-372x^4y^2+18x^4y^4-3036x^2-3036*y^2=0 La triellipse n'est constituée que du triangle central rouge ; les trois courbes bleues, vertes et jaunes correspondent aux équations avec deux signes plus (les quatre autres n'ont pas de points réels). Dans les autres cas, la triellipse n'est qu'une composante connexe ovale de la courbe algébrique en comportant quatre au maximum.
Comme pour l'ellipse, la tangente à la triellipse se construit orthogonalement au vecteur .
Pour , la somme minimale est toujours obtenue en un point unique, appelé point de Fermat-Weber. La n-ellipse est incluse dans une courbe algébrique de degré , pouvant être abaissé à quand n est pair. Ci-contre, la quadriellipse passant par les sommets d'un carré, et la courbe algébrique associée, de degré 16 – 6 = 10.