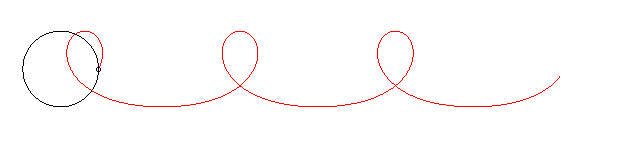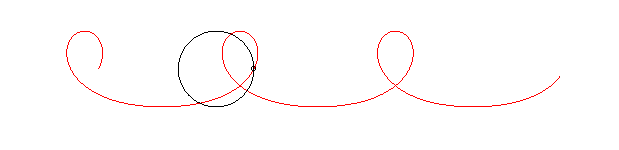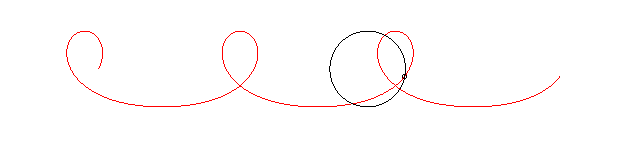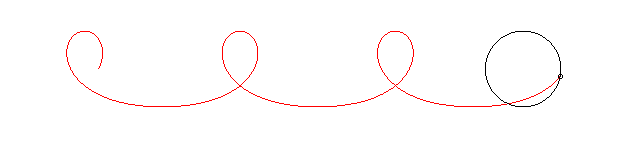
Le nom "courbe de la mascotte" vient de ce que le cercle peut représenter le pourtour d'un régiment, et le point M, un chien, mascotte du régiment, faisant le tour du régiment à vitesse constante.

Ce problème est une variante d'un problème posé par Martin Gardner en 1960 (sous le nom "marching cadets and a trotting dog") dans la revue Scientific American dans le cas d'un régiment carré.

On peut aussi considérer que c'est la courbe décrite par un navire faisant le tour d'un autre en restant à distance constante.
 

Si  et V sont les vitesses respectives du régiment et de la mascotte, R le rayon du cercle,  l'angle repérant la mascotte sur le cercle, les équations horaires du mouvement sont données par : , étant défini, pour une mascotte tournant dans le sens trigo, par l'équation différentielle :  où  et . Paramétrisation cartésienne de la trajectoire : . Distance parcourue par la mascotte lorsqu'elle fait le tour du régiment : (fonction elliptique de deuxième espèce) soit  pour une vitesse de la mascotte double de celle du régiment (k = 2).

La courbe de la mascotte ressemble à une trochoïde à boucle, mais n'en est pas une : cette dernière correspondrait au cas où la mascotte aurait une vitesse constante par rapport au régiment et non par rapport au sol.

Dans l'exemple ci-dessous où la mascotte a une vitesse égale à 1,5 fois celle du régiment, on remarque l'allongement de la courbe entre deux boucles :

© Robert FERRÉOL  2016