Courbe étudiée par P. Huber en 1910 (Loria p. 136) Scyphoïde : en forme de coupe, du grec  scuphos "coupe".

 

Équation cartésienne : . Équation polaire : . Paramétrisation cartésienne :  (). Paramétrisation cartésienne rationnelle :  (). Quartique rationnelle avec point triple en O.

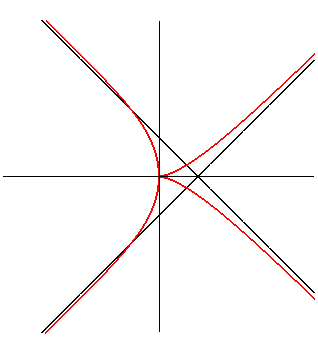La scyphoïde se construit de la façon suivante : une droite variable passant par A(-a, 0) rencontre Oy en P ; la courbe est le lieu des points d'intersection de la perpendiculaire à (AP) passant par P et du cercle de centre P passant par O.
 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2010