Curve studied by P. Huber in 1910 (Loria p. 136) Scyphoid: shaped like a cup, from the Greek scuphos "cup".

 

Cartesian equation: . Polar equation: . Cartesian parametrization: (). Rational Cartesian parametrization: (). Rational quartic with a triple point at O.

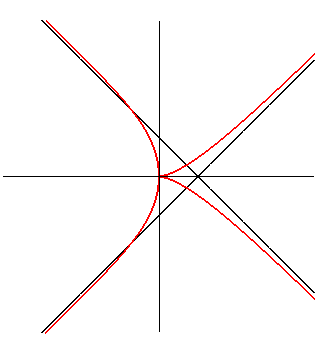The scyphoid can be constructed in the following way: when a variable line passing by A(-a, 0) meets Oy at P; the curve is the locus of the intersection points between the perpendicular to (AP) passing by P and the circle with centre P passing by O.
 
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017