
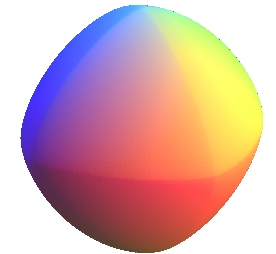
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
LAMÉ SURFACE

|

|
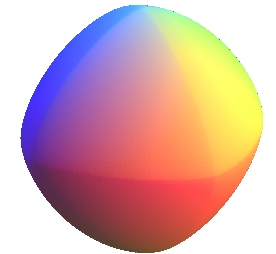
|
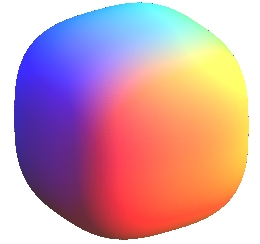
|
|
| Gabriel Lamé (1795-1870): French engineer and
mathematician.
Other name: superellipsoid, quasi-ellipsoidal surface. |
| Cartesian equation of Cartesian parametrization: Volume of the associated ball: |
The Lamé surface
is the "sphere" with radius 1 associated to the norm
;
For rational values of ,
the surface
,
part of
intersected with the eighth of a space
,
is a portion of algebraic surface written
of degree ?? ; when p is even,
and
coincide.
Examples of Lamé surfaces with a = b
=
c:
| octahedral
surface |
plane | |
| sphere: |
same sphere | |
| quartic surface |
||
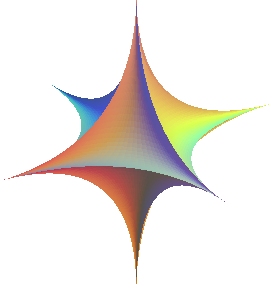
| astroidal surface | surface of degree 18 |
These surfaces can be generalized into the the n-dimensional
hypersurfaces with equation
for which the volume of the associated ball is
;
the case n = 2 is of course the Lamé
curves.
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2021