SURFACE MINIMALE DE CATALAN
Catalan's
minimal surface, Catalansche Minimalfläche
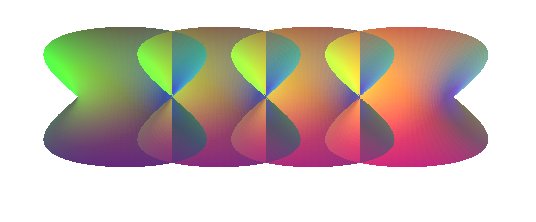
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
SURFACE MINIMALE DE CATALAN
Catalan's
minimal surface, Catalansche Minimalfläche
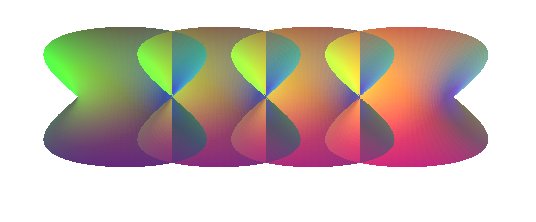
| Surface étudiée en 1855 par Catalan.
Eugène Charles Catalan (1814-1894) : mathématicien franco-belge. |
| Paramétrisation cartésienne : Surface minimale simplement périodique. |
La surface minimale de Catalan est la surface obtenue
en prenant
(puis
)
dans la paramétrisation de Weierstrass d'une surface
minimale :
.
| Si l'on pose De plus, la section de la surface de Catalan par xOy est une cycloïde, qui est une géodésique de la surface. |
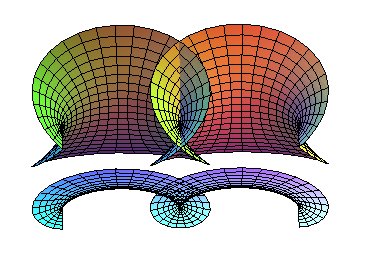 |
| Ci-contre, vue animée des surfaces "associées"
à la surface de Catalan, surfaces obtenues en prenant |
 |
Voici le texte original de Catalan où il publie sa surface comme exemple d'application d'une formule générale pour les surfaces minimales :
Ne pas confondre avec les surfaces de Catalan.
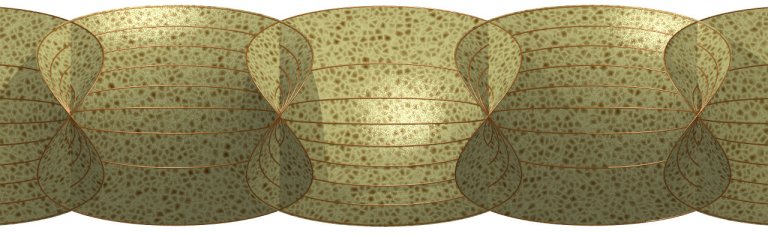
Surface minimale de Catalan, par Alain Esculier
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2012