Il existe de nombreuses généralisations à l'espace des ovales de Cassini, parfois appelées surfaces de Cassini.

Généralisation 1
 
 

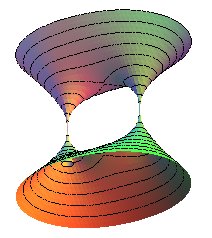
Équation cartésienne :. Surface quartique.

Cette surface a pour courbes de niveau les ovales de Cassini : la courbe de niveau z est l'ovale de Cassini de paramètre b = z de foyers centrés sur les droites . La section par le plan y = 0 est la réunion du cercle  et de l'hyperbole conjuguée . Un exemplaire en bois se trouve au Palais de la découverte, voir cet article.

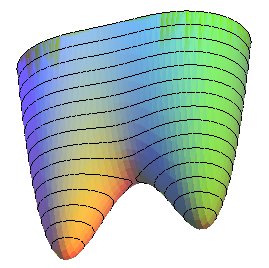
Généralisation 2
 

Une autre surface dont les courbes de niveau sont les ovales de Cassini est la surface d'équation.

Généralisation 3 : cassiniennes 3D à deux pôles
Ce sont les surfaces de révolution obtenues en faisant tourner un ovale de Cassini autour de son grand axe (ici, l'axe Ox) :

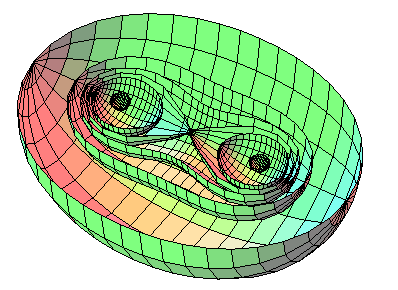
Équation bifocale : , le pôle O étant le milieu des foyers (F', F) , avec a = OF = OF'.  Équation cartésienne : . Surface quartique, non rationnelle pour ab.

Lorsque , la section de la surface par le plan  donne la lemniscate de Booth : .

Généralisation 4
 

Cette fois, on fait tourner l'ovale autour de son petit axe (ici, l'axe Oz). Équation cartésienne : . Pour , la surface est utilisée pour modéliser un globule rouge (voir cette étude). Ci-contre, le cas a = 1,1.b.

 

surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2023