HÉLICOÏDE CERCLÉ
Circled
helicoid, Kreisschraubenfläche

Colonne torse, serpentin, et vis de Saint-Gilles (par Robert
March)
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
HÉLICOÏDE CERCLÉ
Circled
helicoid, Kreisschraubenfläche

Colonne torse, serpentin, et vis de Saint-Gilles (par Robert
March)
| Autre nom : hélicoïde cyclique. |
| Paramétrisation cartésienne : On obtient la vis de Saint-Gilles pour |
Les hélicoïdes cerclés sont les hélicoïdes engendré par le mouvement hélicoïdal d'un cercle.
On distingue trois positions remarquables du cercle générateur
:
 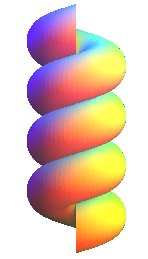
Vis de Saint Gilles : cercle générateur vertical (dans un plan contenant l'axe). |
 |
 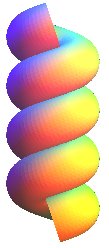 |
| La vis de Saint Gilles dans le cas où l'axe de
l'hélicoïde est un diamètre du cercle ( |
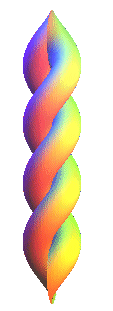  |
Voir aussi les "hélicornes".
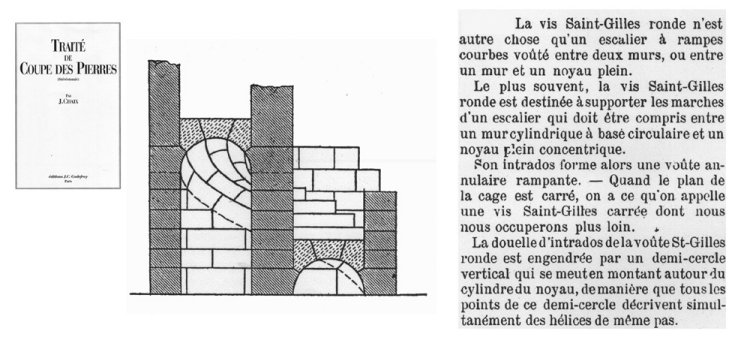



La vis de Saint Gilles originale, près d'Arles

Modèle réalisé par Robert March |
La voûte de cet escalier hélicoïdal est une demi-vis de Saint-Gilles. |

Les colonnes torses (?) de l'autel de Saint Pierre de Rome |

Colonne torse triple |

La colonne serpentine à Istanbul ; quel est son type ???
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2017