Surface cyclotomique

SURFACE CYCLOTOMIQUE
Cyclotomic surface, zyklotomische Fläche

Surface étudiée par Eugène Catalan en 1859 ; nom proposé par Barré de Saint Venant.
Du grec kuklos "cercle" et temnein "couper".

Équation sphérique pour une surface cyclotomique d'axe Oz et de directrice d'équation polaire dans le plan xOy : .
Paramétrisation cartésienne : .
Equation cartésienne : éliminer u entre et , donc de forme générale : .
Equation polaire de la section par un plan z = h : .

Une surface cyclotomique est une surface cerclée engendrée par un cercle de rayon variable en rotation autour d'un de ses diamètres (son centre O restant fixe).

La surface est entièrement définie par la donnée du point O et de la section de la surface par le plan passant par O et orthogonal au diamètre fixe des cercles générateurs, section appelée la directrice de la surface.

Exemples :
Si la directrice est un cercle centré en O, la cyclotomique associée est la sphère.

Si la directrice est un cercle passant par O :

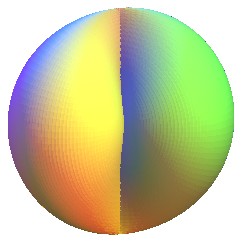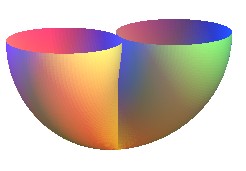Équation sphérique : .
Equation cartésienne : .
Surface quartique.
Équation polaire de la section par un plan z = h : (lemniscate de Both, qui est une lemniscate de Bernoulli pour h = a/2).
Volume : .
Aire : .

Si la directrice est une droite ne passant pas par O :

Équation sphérique : .
Équation cartésienne : .
Surface quartique.

surface suivante surface précédente courbes 2D courbes 3D surfaces fractals polyèdres