Surfaces étudiées par T. Banchoff en 1965, avec W. Kühnel en 1997.

Une surface close orientable est dite tendue si sa courbure de Gauss absolue totale est minimale parmi les surfaces de même genre (cette courbure totale étant définie par  où   est la courbure de Gauss, produit des courbures principales).

Cette valeur minimale est donnée par la formule  où g est le genre de la surface et  sa caractéristique d'Euler Poincaré.

L'inégalité  avec égalité ssi la surface est tendue, est à comparer avec l'égalité de Gauss-Bonnet : .

Le beau théorème suivant caractérise concrètement les surfaces tendues [Kühnel, p. 186] :

Pour une surface close S plongée dans , notant  la partie de S ayant une courbure de Gauss positive, les conditions suivantes sont équivalentes :

a) S est tendue.
b) 
c) 
d) Tout plan sépare S en deux composantes connexes au plus.

En particulier les surfaces tendues de genre 0 sont les surfaces frontières des parties convexes de.
 
 

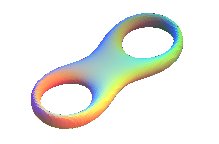
Les tores géométriques sont des surfaces tendues, car tout plan les sépare en deux parties au plus, ou car .	Cette surface de genre 2 n'est pas tendue.	Cette surface de genre 2 proposée par Banchoff et Kuiper en 1981 est tendue (voir [Kühnel, p. 186]). Elle est une composante de la surface d'équation .

 
 
 

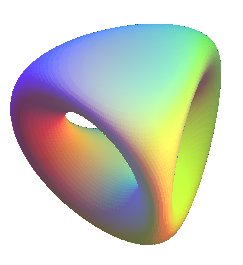surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2019