Paramétrisation cartésienne : (où  ). Surface algébrique rationnelle de degré 16. Première forme quadratique fondamentale : . Élément d’aire : . Courbure totale : 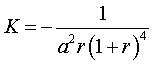. Courbure moyenne nulle (surface minimale).

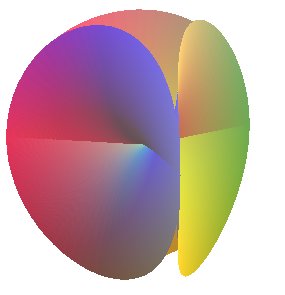
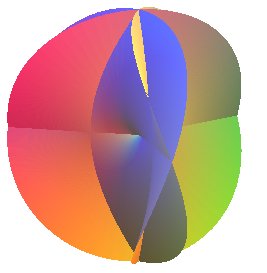
La surface de Bour est la surface minimale obtenue en prenant  dans la paramétrisation de Weierstrass d'une surface minimale : . C'est un cas particulier de surface d'Enneper généralisée.
 

Les projections sur xOy des lignes r = cte sont des hypotrochoïdes à 3 branches.	Comparer avec un demi-cône sinusoïdal :

 
 
 

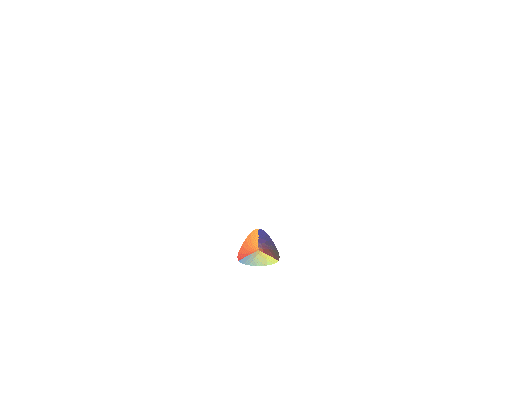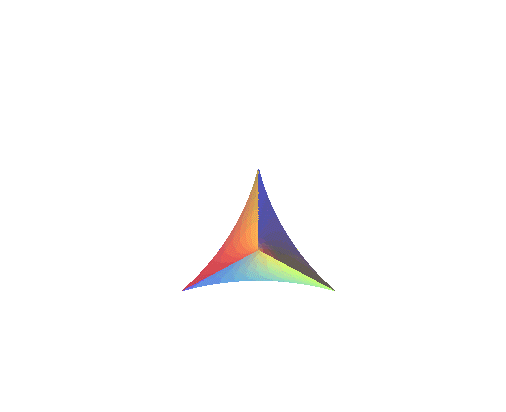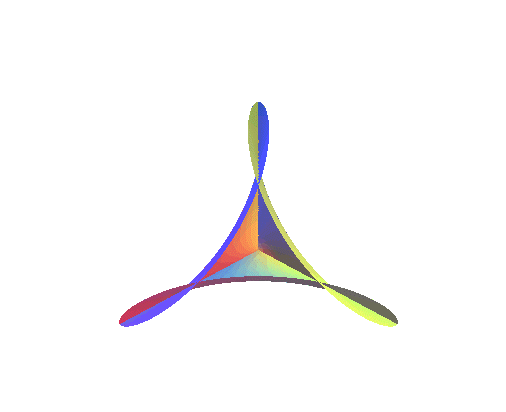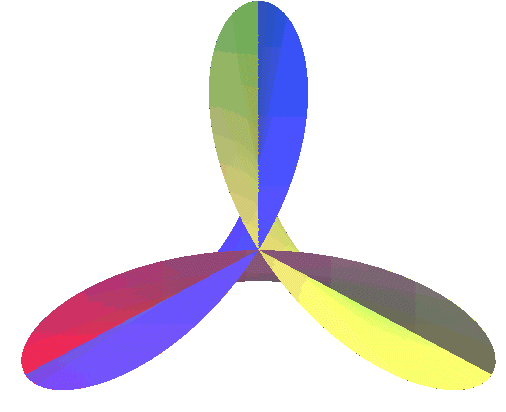surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2011