Curve studied by Loriga in 1910. Juan Jacobo Duran Loriga (1854 - 1911): Spanish mathematician. Texeira III p. 52.

Given a point O and identical punctual light sources placed in the plane, the Loriga curve is the locus of the points of the plane where the illumination due to the n light sources is equivalent to the illumination that would be generated by the n light sources placed at O.

The illumination is inversely proportional to the square of the distance to the source, so it is the curve with punctual equation: .
 

In the case where the n sources are located on the vertices of a regular polygon with radius a, we get, for n = 2, 3, 4 or 5:
 
 

n = 2	Hyperbola
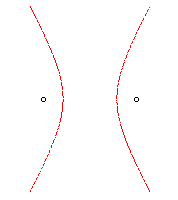n = 3	Loriga quartic. Polar equation:  . Complex equation: . The inflection points are on the circle passing by the sources, and the tangents have the remarkable property visible on the figure: Compare to the Klein quartic.
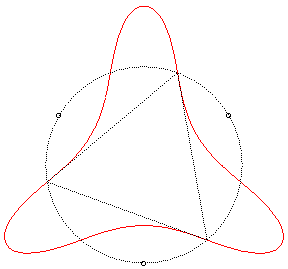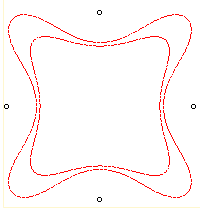
n = 4	Loriga Sextic. Polar equation:
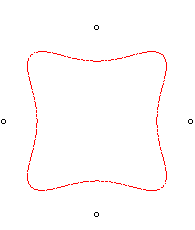n = 5

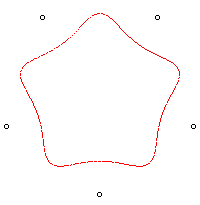Remark: the curve with complex equation  and polar equation, coincides with the Loriga curve only when n = 3, as it can be seen on the following figures:
 

Compare to the isophonic curves and, more generally, see the Goursat curves.
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2017