Sturm spiral

STURM SPIRAL

Curve studied by Sturm in 1857 and Masurel in 2014.
Other name, in this article: Mannheim curve.

The Sturm spirals are the curves such that the radius of curvature is, at all points, proportional to the distance to a fixed point: .
The special case e = 1 is studied on the page dedicated to the Norwich spiral.

Differential equation: (p is the pedal radius).
First integral: , hence the polar equation: .

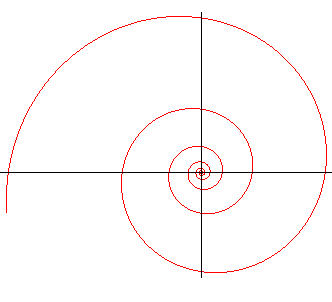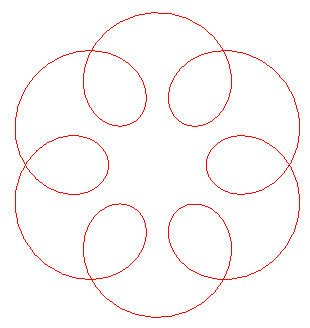
If a = 0, then , which is none other than a logarithmic spiral, with the limit case of the circle for e = 1 (no solution when e < 1).

Elliptic case, e<1
Cartesian parametrization: 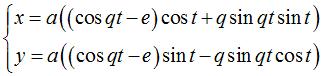where .
Complex parametrization (it is therefore a tritrochoid).
Curvilinear abscissa: . Cartesian tangential angle: .
Radius of curvature:
When q is rational, the order of the rotation symmetry is equal to the denominator of q minus 1.

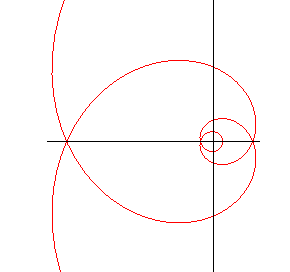
Hyperbolic case, e >1
Cartesian parametrization: where .
Curvilinear abscissa: .
Cartesian tangential angle: .
Radius of curvature: .

Remarkable properties (in the case e = 1 as well):
     - the roulette with linear base of a Sturm spiral is a Duporcq curve with equal parameter e (hence the used of this letter e, associated to the eccentricity of a conic).
    - the evolute of the Sturm spiral in the elliptic case is an epicycloid
    - the evolute of the Sturm spiral in the hyperbolic case is a para- or hypercycloid.

Consider now the curves such that the curvature is proportional to the distance to a fixed point; the differential equation gives the first integral , hence the polar equation .

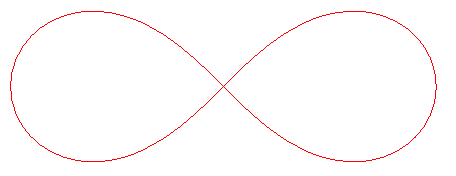
The case c = 0, gives , which is none other than a lemniscate of Bernoulli.
The curvature of a lemniscate is proportional to the distance to its centre.

Finally, one of the solution to is the cardioid.

Compare to the elastic curve, a curve such that the curvature is proportional to the distance to a fixed line, and a certain kind of radioid.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

If a = 0, then , which is none other than a logarithmic spiral, with the limit case of the circle for e = 1 (no solution when e < 1).
Elliptic case, e<1 Cartesian parametrization: where . Complex parametrization (it is therefore a tritrochoid). Curvilinear abscissa: . Cartesian tangential angle: . Radius of curvature: When q is rational, the order of the rotation symmetry is equal to the denominator of q minus 1.
Hyperbolic case, e >1 Cartesian parametrization: where . Curvilinear abscissa: . Cartesian tangential angle: . Radius of curvature: .

Consider now the curves such that the curvature is proportional to the distance to a fixed point; the differential equation gives the first integral , hence the polar equation .
The case c = 0, gives , which is none other than a lemniscate of Bernoulli.	The curvature of a lemniscate is proportional to the distance to its centre.
Finally, one of the solution to is the cardioid.