TAUTOCHRONOUS CURVE

| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
TAUTOCHRONOUS CURVE

| Curve studied by Huygens in 1673 and Newton in 1687.
From the Greek tauto "the same" and chronos "time". |
| A curve joining a point A to a point B
located below is tautochronous if any massive point dropped with
no initial speed on the curve between A and B arrives at
B after a time independent of the initial point.
The solution is a half-arch of a cycloid. |
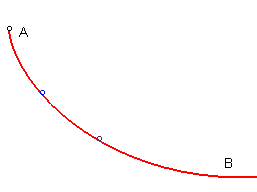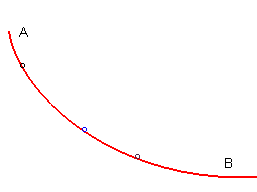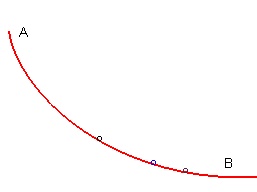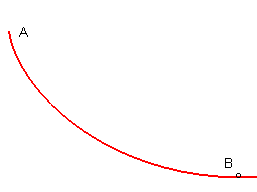 |
The above problem was obviously solved in the case of
a uniform gravitational field.
For the radial gravitational field inside the Earth,
the solution would be a hypocycloid.
See also brachistochrone and isochronous curve.

No matter where you leave from, it will take you the same amount of
time to get to the bottom, but you will not arrive there with the same
speed!
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017