Alysoïde

ALYSOÏDE
Alysoid

Courbe étudiée par Cesàro en 1886 [Nouvelles Annales p.75]
Du grec Alusion "petite chaîne".

Équation intrinsèque 1 :

, b non nul.
Équation intrinsèque 2 :

.
Paramétrisation cartésienne :

, (

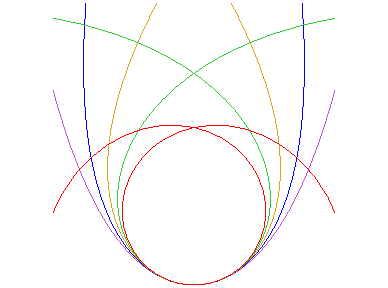
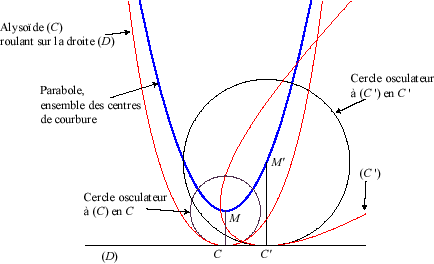
Les alysoïdes sont les courbes telles que lorsqu'on les fait rouler sur une droite, le centre de courbure de la courbe au point de contact décrit une parabole d'axe perpendiculaire à la droite, ne rencontrant pas cette droite (ici, la parabole ) ; voir à courbe de Mannheim.
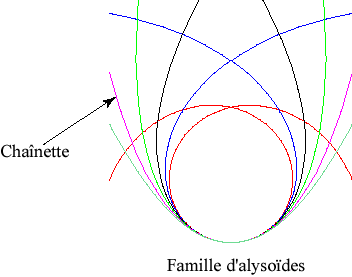
Lorsque a = b (k = 1) , on obtient la chaînette:.
Lorsque a = 2b (k = 1/2), on obtient la paramétrisation : .

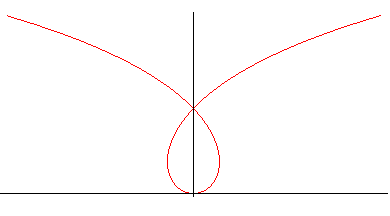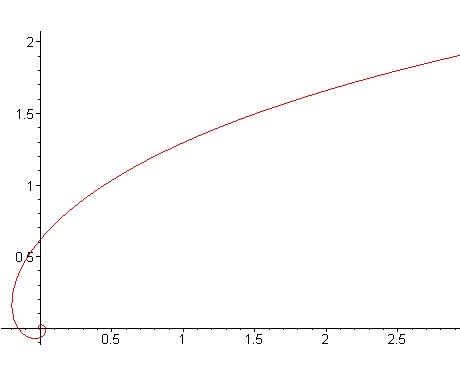
Dans le cas où b est nul, on obtient une courbe différente, cas particulier de pseudo-spirale de Pirondini , dénommée "antiloga", dont les caractéristiques suivent :

Paramétrisation cartésienne :
().

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres