BOHEMIAN DOME
Link to a figure manipulable
by mouse
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
BOHEMIAN DOME
Link to a figure manipulable
by mouse
| Surface studied around 1900 by
A.
Sucharda, professor at a university located in Brno, in... Bohemia.
Other name : circular surface of translation. Virtual images made by Alain Esculier. |
Cartesian parametrization:  .
Cartesian equation:  .
Cylindrical equation:  .
Quartic surface.  .
Area : |
Sections with the planes z= cte |
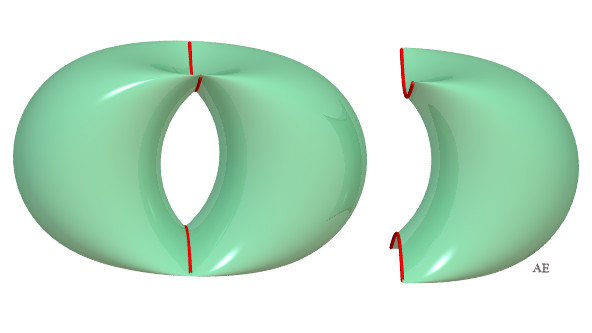
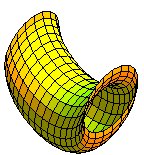
The surface is the reunion of two curved "cylinders",
with volume 
equal to that of the cylinder with radius b and height 2a.
It creates two cavities, with smaller volume because of the self-intersection. |
 |
 |
 |
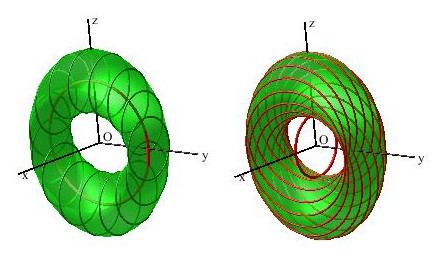
| Given two perpendicular planes P and Q
passing by O (here, yOz and xOz), the associated Bohemian
dome (S) is the circled surface
generated by a circle (here with radius b) the center of which describes
a fixed circle with center O in P (here with radius a)
and the plane of which remains parallel to Q.
As for all the translation surfaces, this definition is symmetrical: (S) is also the surface generated by the circle with radius a the center of which describes a fixed circle with center O in Q and radius b the plane of which remains parallel to P. |
 |
The Bohemian dome is also the Minkowski sum of two circles with perpendicular planes.
The Bohemian dome is an affine projection in 
of
Clifford's torus.
Therefore, it is an immersion in
of the topological torus, but
it is not an embedding of it.
The self-intersection curve is a portion of hyperbola,
with equation:  . |
 |
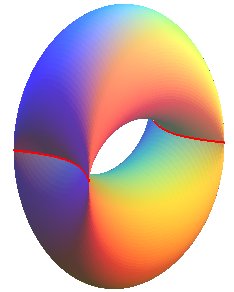This curve degenerates into two segment lines when a = b. |
 |
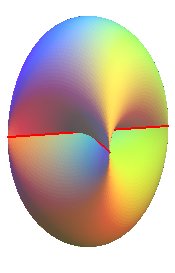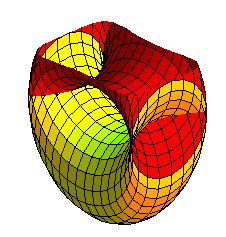
| The case a = b , precisely, is interesting because of its order 4 rotation symmetry: |  |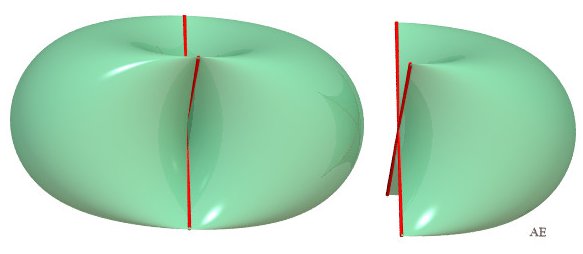
 |
The coordinate lines of the surface under the form 
create a double lattice of ellipses perpendicular two by two. |
 |
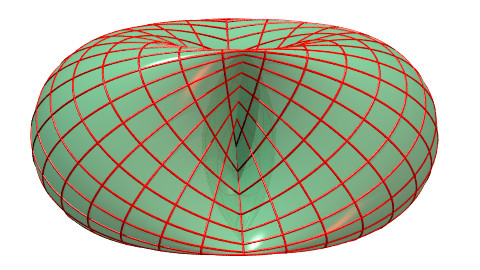| Let's learn how to make the difference between a bohemian vault and a spherical vault! |  |
 |
|
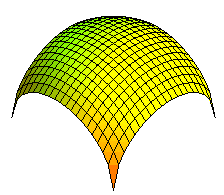Alicante Airport. This website states that the tubes are arches of identical circles, they are therefore bohemian vaults. |
 |
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017
.
