As a topological notion, the torus, or sphere with one handle, refers to any topological space homeomorphic to the Cartesian product of a circle by itself: , like the classic ring torus, or Clifford's torus or , or also the flat polyhedral torus.

Torus obtained by the Maple instruction: tubeplot([cos(t),0,0],t=0..2*Pi,radius=2+sin(t)), close to a sphere with a tunnel

 

Characterization: orientable connected compact surface of genus 1 (or of Euler characteristic zero). Its mean Gaussian curvature is therefore equal to zero.
 

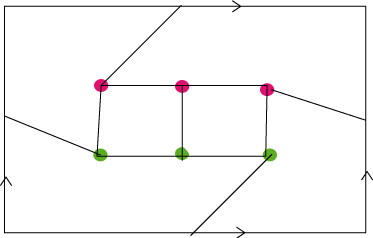
The torus is one of the 3 surfaces obtained by identifying, or in concrete terms, sewing together, the opposite sides of a square:

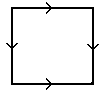
We sew the opposite sides in the same direction: we get a torus.

We sew the opposite sides, a pair of them in the same direction and the other pair not: we get a Klein bottle

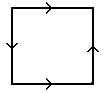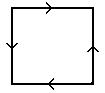We sew the opposite sides in opposite directions: we get a projective plane.

 
 

The chromatic number of the torus (minimum number of colors needed to color the countries of a map traced on the torus so that two countries with a common border have different colors) is equal to the maximum number of countries of a map for which all the countries have, 2 by 2, a common border, and is equal to 7. To get a map of the torus with 7 countries, each touching the 6 others, we can start from a hexagonal pavement for which the hexagons are colored with 7 colors, the 6 hexagons that surround a given hexagon being of different colors. The parallelogram traced with the arrows that indicate the identifications gives a map of the torus with 7 adjacent countries.
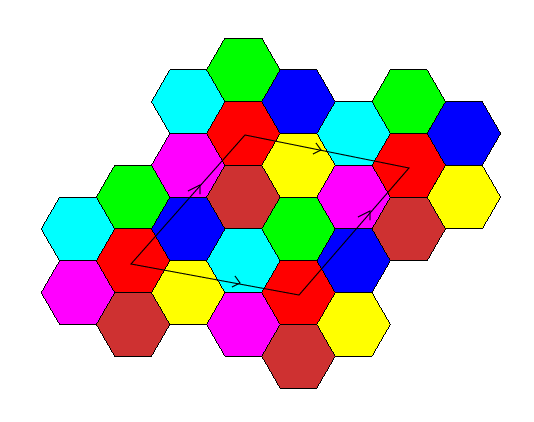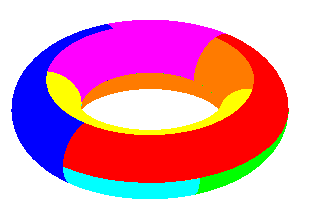
Opposite, an example of a map with 7 countries traced on a "true" torus, each country touching the 6 others. The Szillassi polyhedron achieves the prowess of providing a polyhedral version of this map.
The three utilities problem has a solution on the torus, whereas it cannot be solved in the plane. In other words, the bipartite graph  can be traced on the torus without edges crossing. The same holds for the complete graph with 5 vertices  that the reader will trace easily, but we could also trace the graph  (see Wikipedia). The Csazar polyhedron achieves the prowess of providing a polyhedral version of this graph.

See also the sine surface and the octahemioctahedron which provide immersions of the torus.

This torus can be generalized into the n-dimensional torus.
 
 

next surface

previous surface

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017