KLEIN BOTTLE
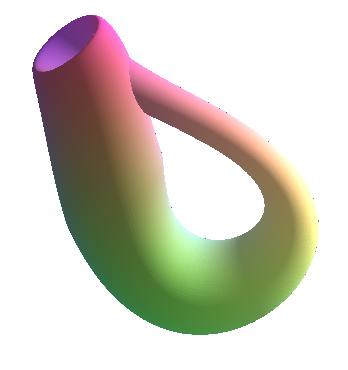
link to a manipulable
figure
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
KLEIN BOTTLE
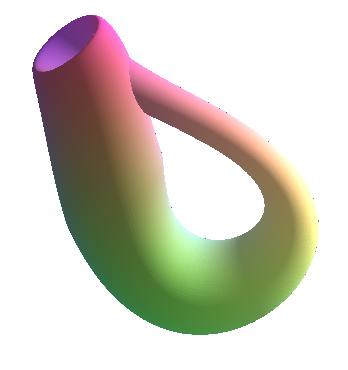
link to a manipulable
figure
| Parametrization without singular points in Parametrization giving the classic form in First part: Second part: Parametrization as a sinusoidal torus (3D projection of the 4D surface above): Rotation of a figure-eight with a twist: Polynomial Cartesian equation of Ian Stewart: See here a general method to create a Klein bottle. |
| The notion of Klein bottle, written |
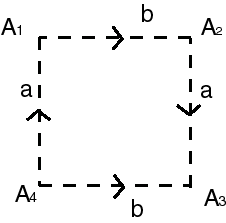 |
| If we begin by identifying the two sides with same direction (in concrete terms, in we sew them together), we get a trunk of cylinder; the Klein bottle is therefore a trunk of cylinder the two boundaries of which are identified with an inversion of direction. |
 |
| If we begin by identifying the two sides with opposite directions, we get a Möbius strip. The Klein bottle is therefore a Möbius strip the two half-boundaries of which are identified in the same direction. (If they are identified with an inversion of direction, we get a projective plane). |
 |
| By using the triangular representation of the Möbius strip, and identifying 2 lower half-bases of the triangle in the same direction, we get the opposite representation of the Klein bottle... |  |
| ...which shows that the Klein bottle is also the surface obtained by sewing two Möbius strips together. | 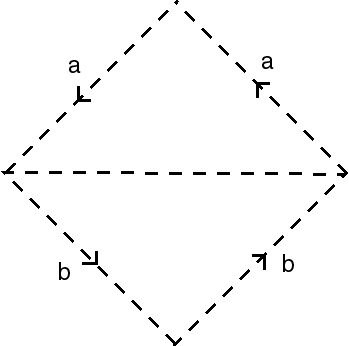 |
| View showing that a half Klein bottle is indeed a Möbius
strip.
|
 |
| Moreover, since the Möbius strip is a punctured
projective plane, the Klein bottle is also the connected
sum of two real projective
planes.
We therefore get another representation of it by adjoining
two open cross-caps:
|

This is also a Klein bottle! |
The Möbius strip is a one-sided
surface (with one face), therefore is not orientable, of genus
2, zero Euler characteristic,
and chromatic number
equal to 6 like the torus:(and
not 7 like the Heawood formula
would indicate)
:
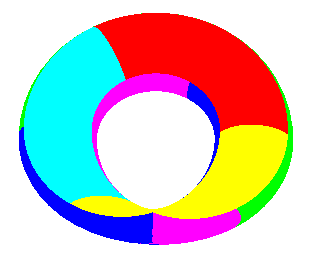

It cannot be embedded in R3, but only immerged with a self-intersection.
Much as the classic representation does indeed look like a bottle (into which one should avoid to pour liquid!),
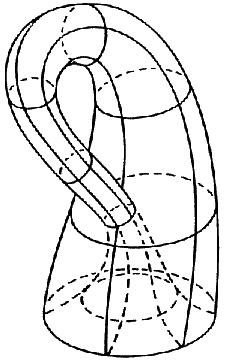
The 3 following representations of the Klein bottle using
this method are more symmetrical than the classic representation, but have
the inconvenient of not having a well-defined tangent plane at some points:
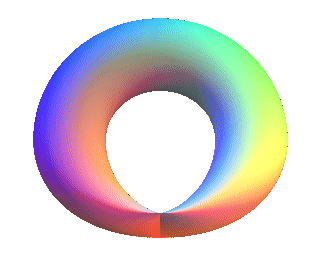 |
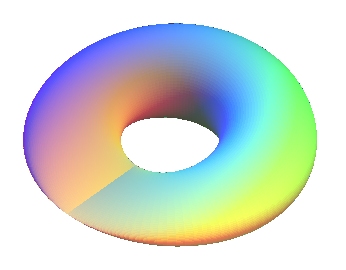 |
 |
| Collage of a half torus with a half Bohemian
dome.
There are two cuspidal points. |
Sine torus.
Two cuspidal points too. |
Tube with a bore shaped like a piriform
quartic.
There is a cuspidal line. |
| Rotation of a figure-eight curve with a half-twist; we get this time a real immersion of the Klein bottle, not at all shaped like a bottle! |
 |
 |
| The first representation allows to see how the Klein bottle is obtained by identification of two half-boundaries of a Möbius strip: |  |
The second representation allows to see how the Klein bottle is obtained by sewing two Möbius strips together.
 +
+ |
 =
= |
 |
In ,
the movement of a circle with a twist can be carried out without the resulting
surface presenting self-intersections (see the parametrization in the above
box).
Finally, here is a polyhedral model of the Klein bottle:
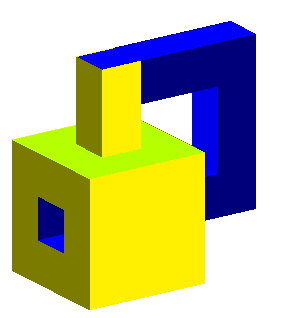
If we paint the Klein bottle, the layer of paint obtained
(which is in one piece since the surface is one-sided) is an immersion
of the torus (in other words, the two-sheeted
covering is the torus); it is the reason why the Klein bottle was used
as a central step for turning the torus inside out: see for example this
text in Pour la Science.
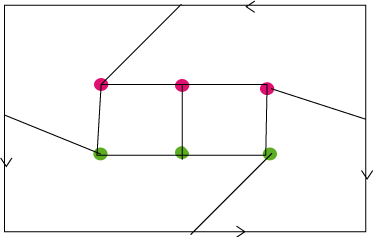
| The three
utilities problem can be solved on the Klein bottle, whereas it cannot
be solved on the plane. In other words, the bipartite graph The same holds for the complete graph with 5 vertices |
 |
The punctured Klein bottle (characterized by the fact
that it is a one-sided surface of genus
2 with a boundary) can be represented by the Möbius shorts:
we get it by connecting a closed strip with no twists by a band like below:
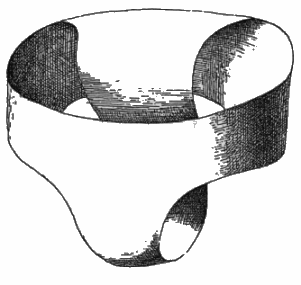
These shorts, impossible to put on, are a punctured Klein bottle! |
 |
| Just as the Möbius strip can be generalized into
a strip with n half-twists (and we topologically get a Möbius
strip only when n is odd), the Klein bottle can be generalized into
a bottle with n twists, which is topologically a Klein bottle only
when n is odd.
Opposite, the multiple bottles were created from a tube with variable section the bore of which is an epicycloid. |
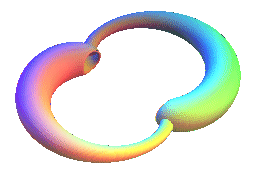
 |
The Klein bottle enables computer graphics designers to display their talent:
LINKS:
www.geom.uiuc.edu/~banchoff/Klein4D/Klein4D.html
Games on a Klein bottle: geometrygames.org/TorusGames/index.html
To buy glass Klein bottle and even a Klein cap!:
www.kleinbottle.com
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017