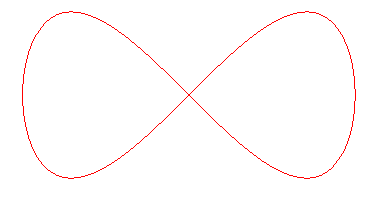
LEMNISCATE DE GERONO, ou HUIT
Gerono's
lemniscate (or eight curve), Geronosche Lemniskate
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
LEMNISCATE DE GERONO, ou HUIT
Gerono's
lemniscate (or eight curve), Geronosche Lemniskate

| Courbe étudiée par Grégoire de St
Vincent en 1647 et Cramer en 1750.
Nom donné par Aubry en 1895. Camille-Christophe Gerono, 1799 - 1891 : mathématicien français. |
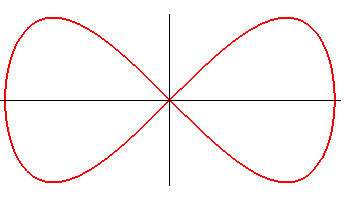 |
Paramétrisation cartésienne : Équation cartésienne : |
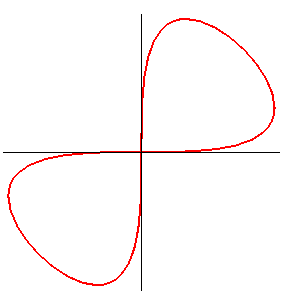 |
Paramétrisation cartésienne de l'image par une rotation de |
 |
L'image par une affinité de rapport Voir la poire de Tannery. |
La lemniscate
de Gerono est un cas particulier de besace
(voir cette page pour une construction) et de courbe
de Lissajous (cf. la paramétrisation : ).
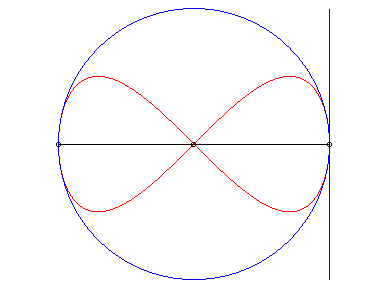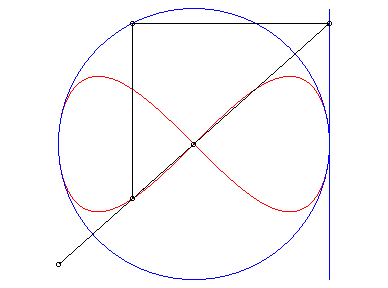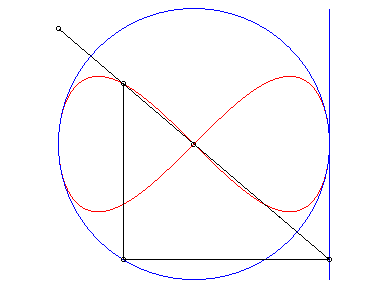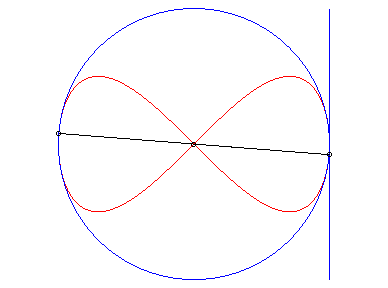
| La lemniscate de Gerono est l'antihyperbolisme d'un cercle par rapport à son centre et une tangente. |
 |
|
Elle s'obtient aussi par transformation de Newton à partir de deux cercles tangents comme illustré ci-contre : |
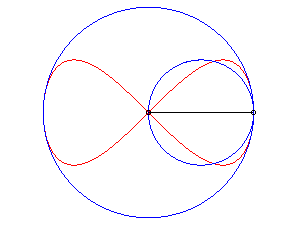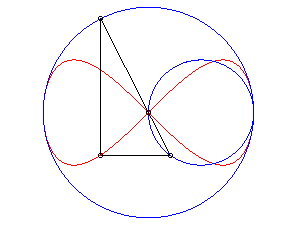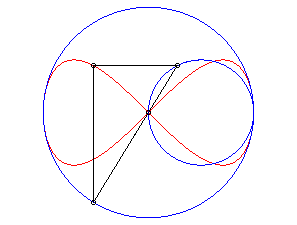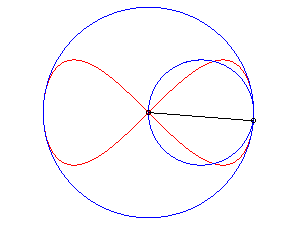 |
| Autre construction, due à L. I. Magnus : Un point P décrivant un cercle de centre O, on projette P en Q sur un diamètre, puis Q en R sur (OM); la lemniscate de Gerono est le lieu du point M de [PQ] tel que QM = QR. |
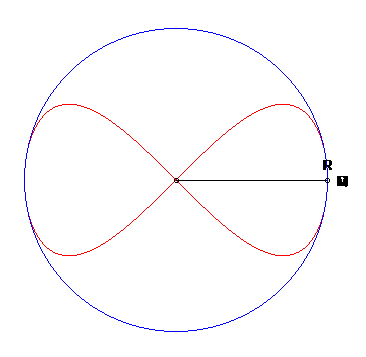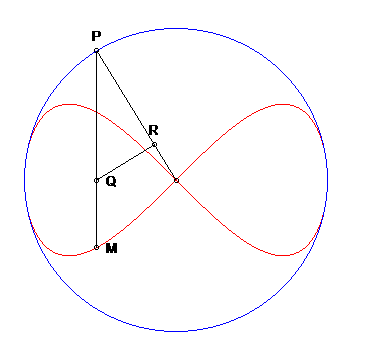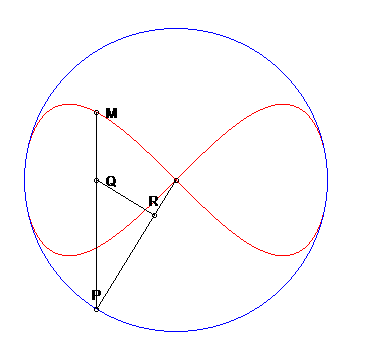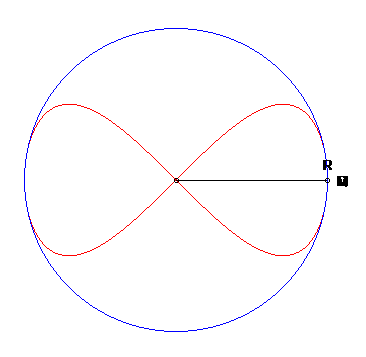 |
| L’équation |
 |
Comme toute courbe de Lissajous, La lemniscate de Gerono
est la projection de deux couronnes
sinusoïdales :
1) Projection sur xOy de la courbe
de la crêpe, de paramétrisation : .
2) Projection sur xOy de la fenêtre
de Viviani : .
Plus généralement, la lemniscate de Gerono
est une vue de l’hippopède,
intersection d’une sphère avec un cylindre tangent.
| La lemniscate de Gerono peut être obtenue à partir de celle de Bernoulli de la façon suivante : tracer sur la sphère de centre O et de rayon a la courbe ayant la lemniscate de Bernoulli comme stéréographique de pole sud (courbe qui est la courbe de Viviani), et projeter cette courbe orthogonalement sur xOy. | 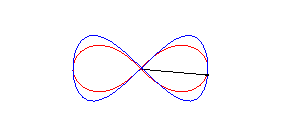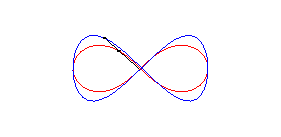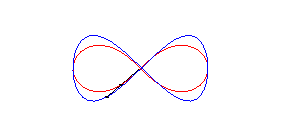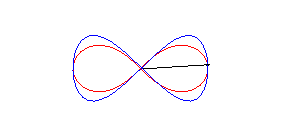 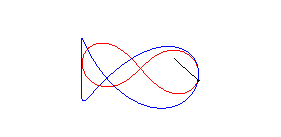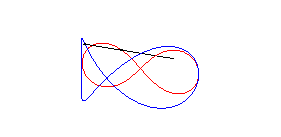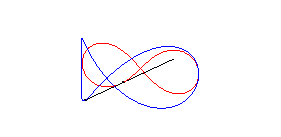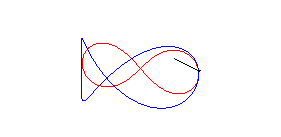
|
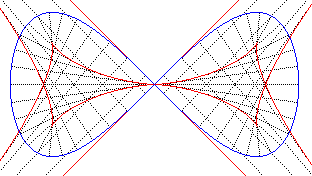
| Une différence entre la lemniscate de Gerono et celle de Bernoulli : la première possède 6 sommets (4 maximums de courbure et deux minimums) comme le montre la vue ci-contre avec sa développée ; celle de Bernoulli ne possède que deux sommets, aux deux extrémités. |
 |
Voir aussi :
- la poire
de Tannery, rotation d'un demi-huit autour de son axe.
- la bouteille
de Klein dont une représentation peut se faire à partir
d'un huit, de même que le pseudo-bonnet
croisé.
Surfaces de révolution autour des axes de symétrie.
| 1) Autour de l'axe passant par les sommets,
d'équation, et de paramétrisation cartésienne : |
 |
| 2) Autour de l'autre axe,
d'équation, et de paramétrisation cartésienne
:
|
|
| Si l'on change l'équation |
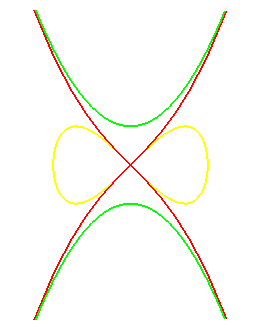 |
| Si l'on change |
 |
L'image par une dilatation de la lemniscate de Gérono  est parfois appelée lemniscate de Montferrier ; équation
cartésienne :
est parfois appelée lemniscate de Montferrier ; équation
cartésienne : |
 |
Voir ici comment
"épaissir" un huit :  .
.
Les sections de la surface d'équation
par des plans x=cte ou y=cte sont des huits dilatés
:

| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2022