Courbe étudiée par Jacques Bernoulli en 1694 et Fagnano en 1750. Jacques Bernoulli (1654 -1705) : mathématicien suisse. Lien vers un article de Math OS.

 

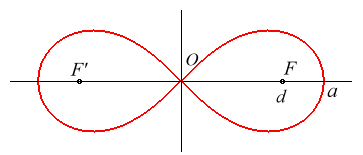Équation bipolaire :  (où d est la demi-distance entre les pôles F et F', foyers de la lemniscate). Équation tripolaire :   (O milieu de F et F'). Équation polaire :  (avec  , F(d, 0), F'(-d,0)).

Équation cartésienne : . Quartique bicirculaire rationnelle. Paramétrisation cartésienne par fonctions circulaires :  (). Paramétrisation cartésienne rationnelle :  (,  ), soit en complexes : . Paramétrisation cartésienne par fonctions hyperboliques :   (). Autre paramétrisation cartésienne :  (). Équation complexe :  ou . Équation podaire : . Angle tangentiel polaire : . Abscisse curviligne : . Rayon de courbure : . Équation intrinsèque :. Longueur : , où , intégrale elliptique de première espèce, est la constante de la lemniscate (prononcer "pi script"), à rapprocher de . On a aussi :  . Aire totale : a2.

La lemniscate de Bernoulli dispute à la cardioïde le record du nombre d'appartenances aux diverses familles de courbes remarquables.

Elle est en effet :

- un cas particulier d'ovale de Cassini (voir l’équation bipolaire)
- un cas particulier de courbe de Booth.
- un cas particulier de spirale sinusoïdale (voir l’équation polaire)
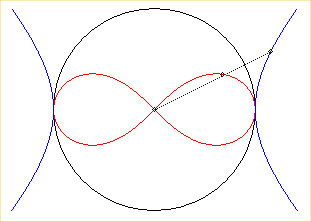
- comme toute quartique bicirculaire rationnelle : à la fois podaire par rapport à O et inverse (cercle d'inversion de diamètre [A(a,0) ; A'(–a,0)]) de l’hyperbole équilatère de centre O et de sommets A et A' ; F et F' sont les inverses des foyers de cette hyperbole et les tangentes à l'origine, les inverses des asymptotes.
- c'est donc aussi, en tant que podaire, l’enveloppe des cercles de diamètre d'extrémités son centre et un point de cette hyperbole.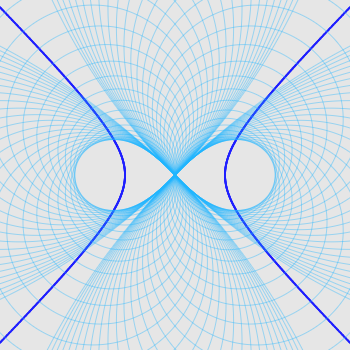
- ainsi que le lieu du centre d'une hyperbole roulant sans glisser sur une hyperbole égale, avec des sommets coïncidants.
- la cissoïdale du cercle de centre F passant par O et du cercle de centre  et de rayon a.
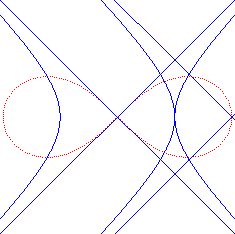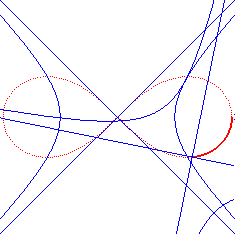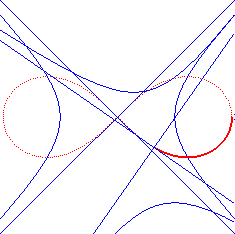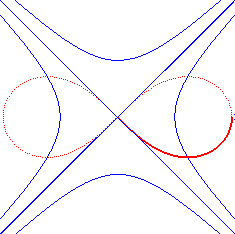
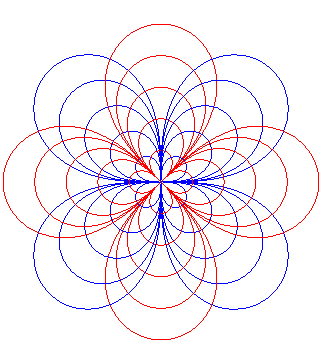
- la cissoïdale de pôle O des cercles (C) et (C') de centres F et F' et de rayon a/2. En pointillé les cercles (C) et (C'), en bleu leurs homothétiques dont la lemniscate est la médiane.
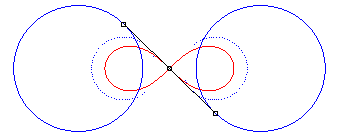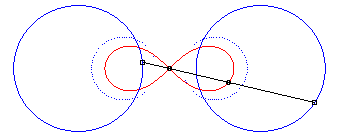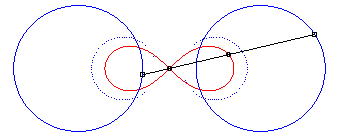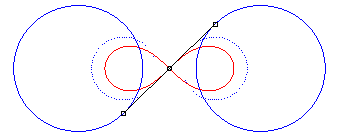- le lieu des milieux des segments de longueur 2d dont les extrémités décrivent les deux cercles de rayon a centrés en F et F'.
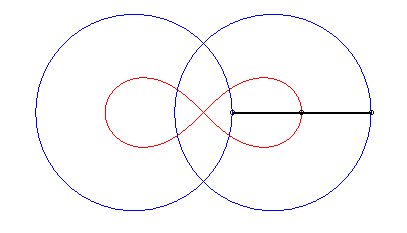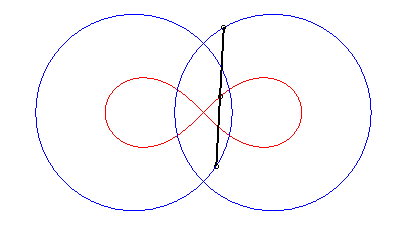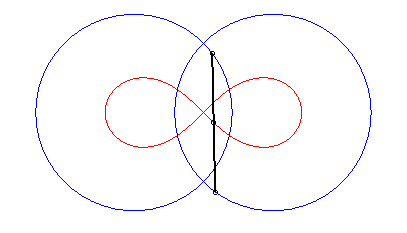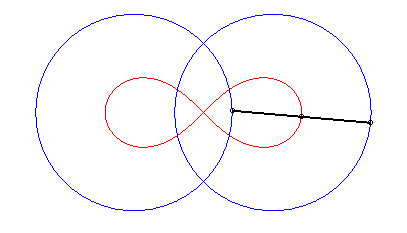La lemniscate est donc une courbe du trois-barres, dans le cas particulier de la courbe de Watt ; d'après le principe de l'échange bielle manivelle, il existe une deuxième construction avec quadrilatère articulé :
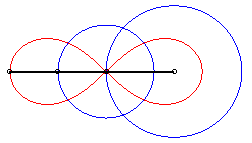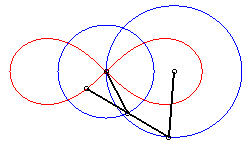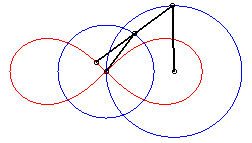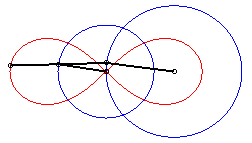Deux points A et B coulissant sur deux axes perpendiculaires en O de sorte que le triangle OAB ait une aire constante, le lieu du projeté M de O sur [AB] est un lobe de lemniscate de Bernoulli. Nota : la droite (AB) enveloppe une hyperbole équilatère, décrite par le milieu de [AB]. Équation polaire :  où S est l'aire du triangle ; coordonnées de A : , coordonnées de B : . Source : AMM 1920 .
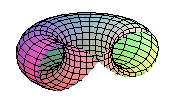
La lemniscate est encore : - la section d'un tore, de rayon de révolution d et de rayon de méridienne d/2, par un plan situé à une distance d/2 de l'axe (la lemniscate est donc une spirique de Persée)
- la courbe passant par O dont la courbure est proportionnelle à la distance à O (comparer avec la courbe élastique, dont la courbure est proportionnelle à la distance à une droite fixe)
- le lieu des points M tels que
- la projection sur le plan xOy de la biquadratique :  , intersection d'un cône de révolution et d'un paraboloïde de révolution :

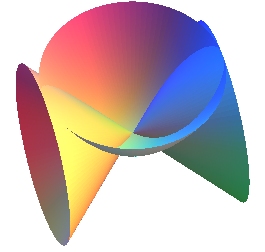D'autre part :

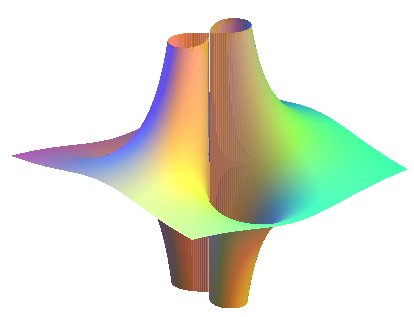
- les courbes asymptotiques du conoïde de Plücker se projettent suivant des lemniscates de Bernoulli.

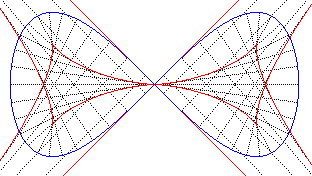
- la lemniscate de Bernoulli est une courbe synodale de toutes ses sécantes issues du point double :

- Les sections horizontales des deux surfaces associées à la fonction complexe , d'équations  sont des lemniscates de Bernoulli :

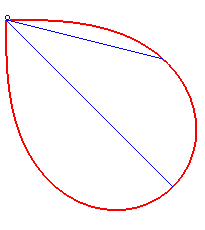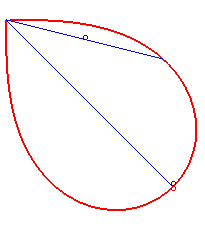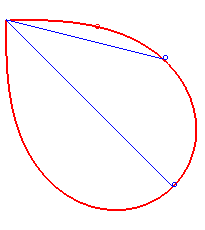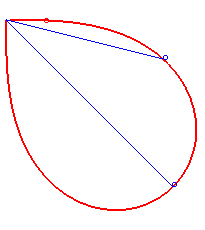
La développée de la lemniscate de Bernoulli a pour paramétrisation . On constate que les deux sommets correspondent à des maximums de courbure...
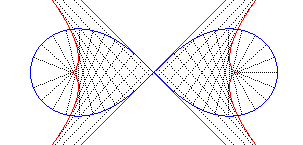...contrairement à la lemniscate de Gerono où ils correspondent à des minimums...
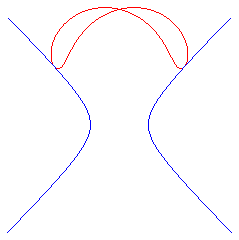
Extension : la podaire de l'hyperbole équilatère par rapport à un point de l'axe de symétrie est une lemniscate déformée, de paramétrisation .

Mécanisme de Watt pour construire la lemniscate

Familles de lemniscates orthogonales

Voir ici comment "épaissir" une lemniscate:.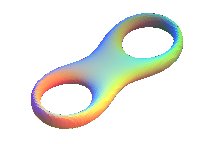

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2021