Équation cartésienne réduite :  avec A > B, soit . Quartique bicirculaire, rationnelle si C = 0, n'ayant de points réels que si . Équation polaire : .

Les spiriques de Persée sont les quartiques bicirculaires ayant un centre de symétrie. Ce sont les donc les cycliques dont la déférente est une conique à centre, par rapport au centre de cette conique,  autrement dit les enveloppes de cercles dont le centre décrit une conique à centre, et tels que le centre de la conique a une puissance constante par rapport à ces cercles.
 
 

Cas 0 < B < A fixés, C variant de moins l'infini à A2 , cas du tore croisé. Pour , les courbes sont des ovales (courbes jaunes), pour C = 0 on obtient un ovale de Booth (en violet), avec point isolé au centre, pour , courbes à deux composantes, un haricot et un ovale (en bleu), pour , réunion des cercles de centres , de rayon , pour , les courbes, bien que réelles, ne correspondent plus à des sections de tore réel, pour , courbes à deux composantes non convexes (vertes), pour , courbes à deux composantes convexes (cyanes), pour , courbes réduites à deux points .

Cas -A < B < 0 < A fixés, C variant de moins l'infini à A2, cas du tore ouvert Pour , les courbes ont des formes d'ovales puis de haricot (courbes jaunes), pour C = 0 on obtient un ovale de Booth (en violet), pour , courbes à deux composantes(en bleu), pour , réunion des cercles de centres , de rayon , pour , les courbes, bien que réelles, ne correspondent plus à des sections de tore réel, pour , courbes à deux composantes non convexes (vertes), pour , courbes réduites à deux points .

Historiquement ces courbes ont été définies comme sections d'un tore par un plan parallèle à son axe ; mais pour obtenir toutes les courbes réelles données ci-dessus, il faut accepter de considérer des tores complexes.
Pour un tore de centre O, d'axe Oz, de rayons majeurs et mineurs a et b, coupé par le plan parallèle à Oz situé à une distance d de O, on obtient dans un repère d’origine le projeté de O sur ce plan l'équation cartésienne ci-dessus avec : .
Ceci provient de l'équation :  de ces courbes.

On constate alors que le tore ci-dessus n'est réel que si .
 

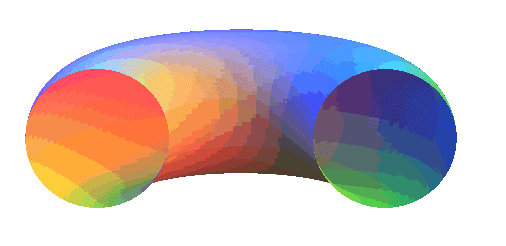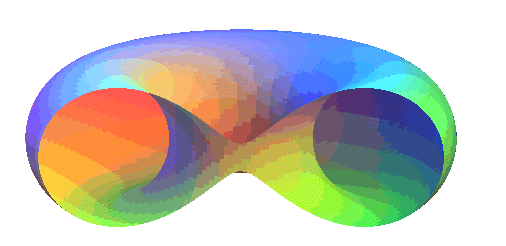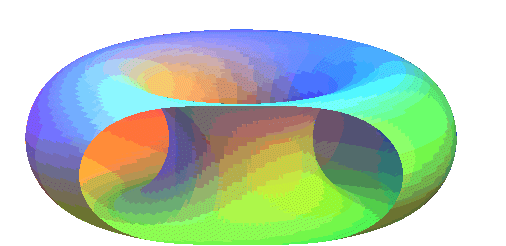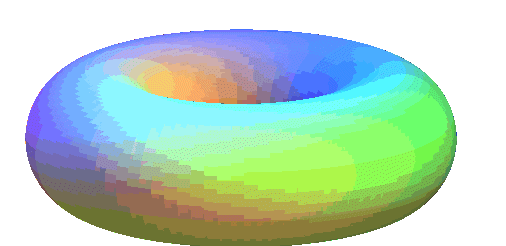
Spiriques de Persée de tore ouvert

Spiriques de Persée de tore croisé

Lorsque , soit d =  b (distance du plan à l'axe égale au rayon mineur), on obtient les ovales de Cassini, qui se réduisent à la lemniscate de Bernoulli lorsque  C = 0, soit a  = 2 b.
Lorsque C = 0, soit  (plan tangent intérieurement au tore), on obtient les courbes de Booth (ou hippopèdes de Proclus), qui se réduisent également à la lemniscate de Bernoulli lorsque a  = 2 b.

Le cas limite A = B (cas où le tore est réduit à une sphère) donne des cercles.

Les spiriques de Persée sont aussi les isoptiques des coniques à centre.
 

Les courbes d'équation tripolaire  où O est le milieu de [FF'] forment une sous-famille à un paramètre des spiriques de Persée.
En effet dans le repère où  et  ces courbes ont pour équation : , donc pour cette famille :
.
 
 
 

Les courbes ne correspondent à des sections de tore réel que pour . Pour , on obtient les deux "foyers" F et F', pour , courbe à deux composantes ovales (vertes), pour , courbes à deux composantes non convexes (rouges), pour k = 2, réunion de deux cercles de centres les foyers et de rayon , pour k > 2, courbes à deux composantes (cyanes)

 

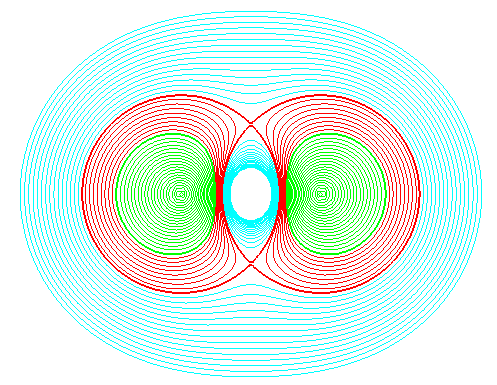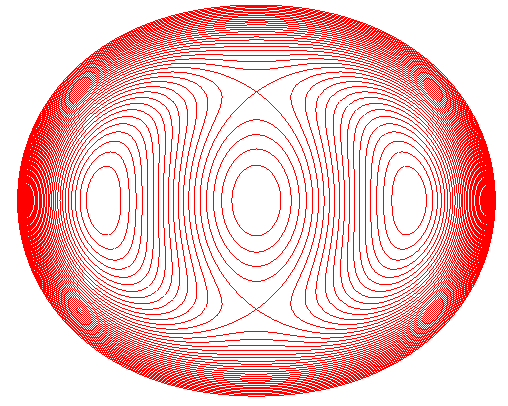
Disque en matière biréfringente chargé diamétralement et observé en lumière monochromatique polarisée. Les lignes noires - les isochromatiques - sont les lieux des points pour lesquels la différence des 2 contraintes principales est constante. Photo de M. Konieczka et Mme Gautherin, laboratoire de Mécanique du Département de Génie Mécanique de l'ENS de Cachan

 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2024