Notion étudiée par Apollonius, vers 200 av. J.C. puis par Huygens en 1673. Autres nom : focale, ou caustique.

La développée d’une courbe est le lieu de ses centres de courbure, ou encore l’enveloppe de ses normales.
 

Pour une courbe de départ :  de point courant  la développée est l'ensemble des points . Paramétrisation cartésienne :  Paramétrisation complexe : . Si la courbe de départ a pour équation intrinsèque 2 : , on obtient : Équation intrinsèque 1 paramétrique : . Équation intrinsèque 2 :.

Interprétation cinématique : la développée est la base du mouvement plan sur plan dont le plan mobile est le plan emmené par la tangente à la courbe. La roulante en est la normale, qui roule donc sans glisser sur la développée.
 

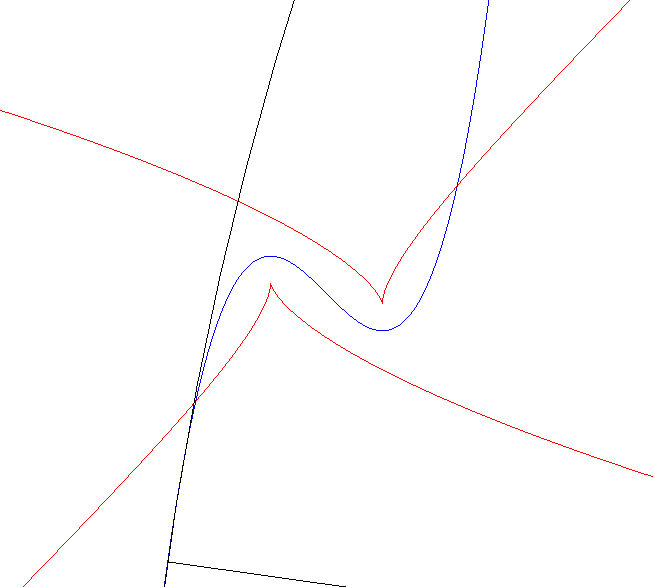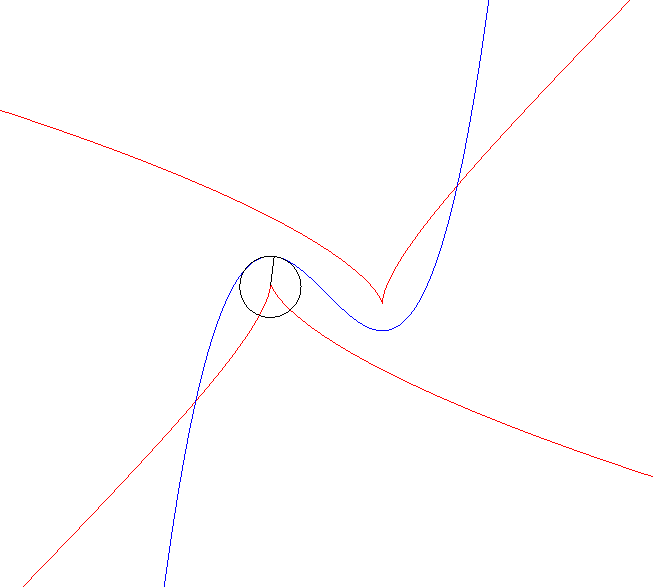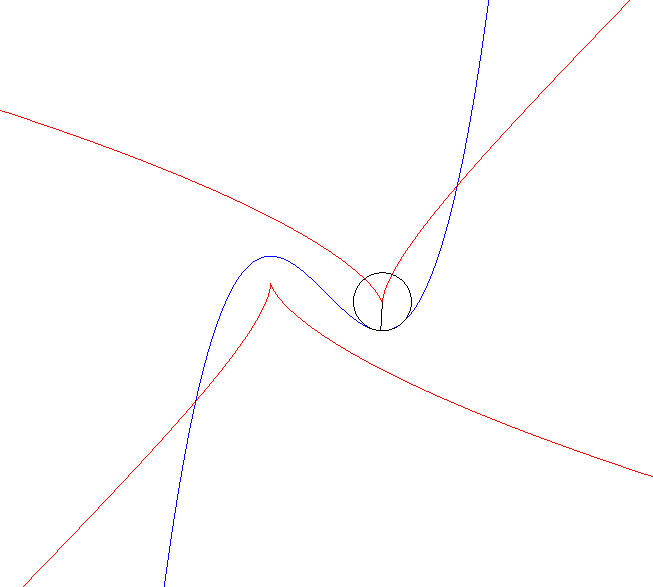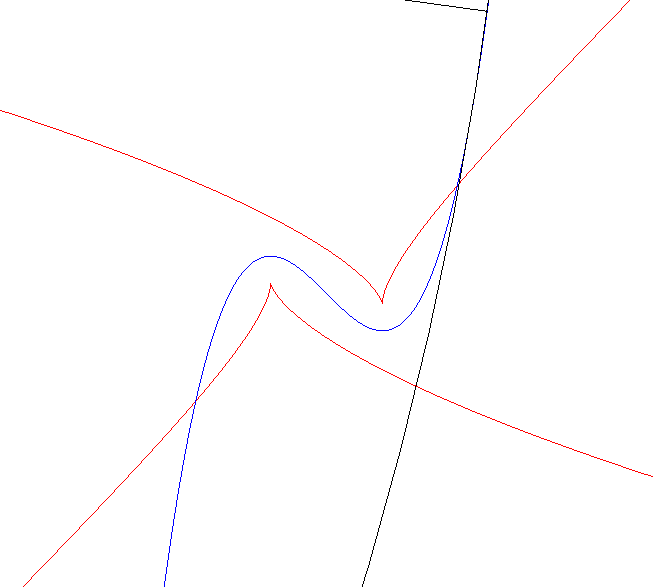
Les points singuliers de la développée correspondent aux sommets de la courbe, c’est-à-dire aux extremums du rayon de courbure, notion généralisant celle de point situé sur un axe de symétrie avec tangente perpendiculaire à cet axe. Ci-contre, on constatera deux minimums non nuls et un maximum infini du rayon de courbure ; dans ce dernier cas, le point singulier est à l’infini, et la normale est asymptote à la développée. A droite, animation avec le cercle de courbure.

Les développées de 2 courbes semblables sont semblables (avec la même similitude) ; la développée d'une courbe algébrique est une courbe algébrique.

Interprétation physique : la courbe  étant une source lumineuse, la développée représente le lieu où sont concentrés les rayons lumineux émis par la courbe ; la développée est donc appelée plutôt caustique en optique (mais voir la définition voisine de la caustique en maths) ; elle est aussi le lieu des points singuliers des fronts d'onde issus de  (voir à courbes parallèles).

La développée de la courbe orthotomique de  par rapport à un point S (elle-même image de la podaire de  par rapport à S dans une homothétie de centre S et de rapport 2), est la caustique par réflexion de centre S de , soit en raccourci :

Il y a donc par exemple identité entre les développées de limaçons de Pascal et les caustiques de cercle.

Exemples :
 

courbe de départ	développée
ellipse	tétracuspide  avec
hyperbole	1/2 courbe de Lamé : avec
parabole	parabole semi-cubique
cycloïde	la même cycloïde translatée
cardioïde	cardioïde semblable dans le rapport 1/3
néphroïde	néphroïde semblable dans le rapport 1/2
épicycloïde de paramètre q	épicycloïde semblable dans le rapport q/(q + 2)
deltoïde	deltoïde semblable dans le rapport 3
astroïde	astroïde semblable dans le rapport 2
hypocycloïde de paramètre q	hypocycloïde semblable dans le rapport q/(q – 2)
paracycloïde	hypercycloïde
hypercycloïde	paracycloïde
spirale logarithmique :	spirale logarithmique
tractrice	chaînette
spirale tractrice	courbe de Catalan
chaînette	courbe
sextique de Cayley	néphroïde
spirale de Norwich	développante de cercle

Voir aussi à développante, voir une généralisation plane à développoïde, voir la notion de développée d'une courbe 3D,  la notion de surface polaire et la notion de focale qui est aux surfaces ce qu'est la développée aux courbes.
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2022