English version

Les hypocycloïdes sont les courbes décrites par un point d'un cercle (C) roulant sans glisser sur et intérieurement à un cercle de base (C₀), le cercle roulant étant plus petit que le fixe ; ce sont donc des cas particuliers d'hypotrochoïdes.

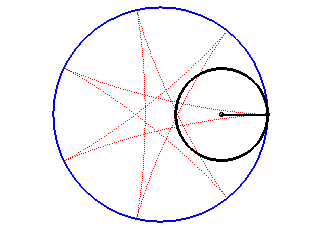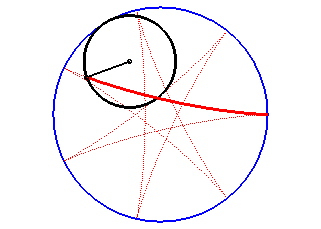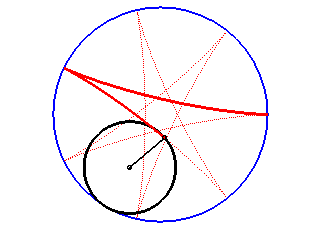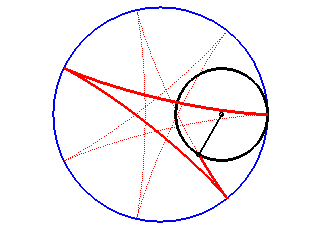
Paramétrisation complexe :  où a est le rayon du cercle de base et  celui du cercle roulant (q > 1). Paramétrisation cartésienne : . Rayon vecteur :  ; angle polaire donné par . Abscisse curviligne donnée par  (d'où l'équation différentielle : ).  Deux expressions possibles pour l'abscisse curviligne :  1)  2) . Angle tangentiel cartésien : 1)  ou 2) . Rayon de courbure : 1)  ou 2)  Équation intrinsèque 1 (forme 1) : . ( est l’équation d’une hypocycloïde si et seulement si d < c, avec ) Équation intrinsèque 2 (forme 1): . ( est l'équation d'une hypocycloïde si et seulement si |B| > 1). Équation podaire : . Equation de la tangente en M(t) : . Longueur d’une arche : . Aire de la surface située entre l'arche et les deux tangentes à ses extrémités : . Pour q entier, la longueur totale vaut donc  fois la longueur du cercle de base, et  l’aire totale vaut  fois l’aire de ce cercle.

Les hypocycloïdes sont des courbes formées d'arcs isométriques (les arches) se rejoignant en des points de rebroussements (obtenus pour ) en nombre égal au numérateur du nombre q si q est rationnel et en nombre infini sinon.
Lorsque q est rationnel, , la courbe est algébrique rationnelle (prendre comme  paramètre ).
Elle a la même structure qu'un polygone régulier, croisé si m ³ 2, à n sommets joints de m en m par des courbes situées à l'intérieur du cercle (C₀).

Lorsque l'on parle d'hypocycloïde simple à n rebroussements (E_n), on considère le cas q = n, c'est-à-dire celui où il n'y a pas de croisement.

Si l'on prend 0 < q < 1 dans les formules ci dessus, le cercle roulant est plus grand que le cercle de base ; on est donc dans le cas des péricycloïdes, qui sont aussi des épicycloïdes dont le rapport du cercle de base au cercle roulant vaut  ( donc si l'on prend  dans les formules ci dessus, on obtient l'épicycloïde à n rebroussements).

Pour q > 1, lorsque l'on change b en a – b (soit q  en  ou  en  dans le cas rationnel), la courbe n'est pas modifiée. Ceci constitue la propriété de double génération de l'hypocycloïde :

On obtient donc toutes les hypocycloïdes possibles en prenant seulement b £ a/2 , soit q ³ 2 :
On remarquera que l'hypocycloïde de paramètre q = a/ b  irréductible a la même forme que le polygone régulier croisé de symbole {a/b}
 

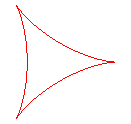
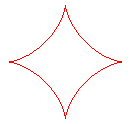
q = 1 : point	q  = 2 : droite de La Hire	q = 3 : deltoïde	q = 4 : astroïde	q = 5
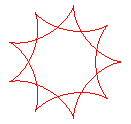
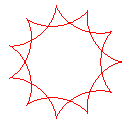
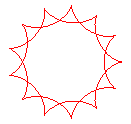
q = 5/2 : hypocycloïde étoilée à cinq rebroussements	q = 7/2	q = 9/2	q = 11/2	q = 13/2
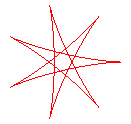
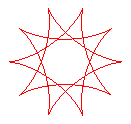
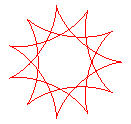
q  = 7/3	q = 8/3	q = 10/3	q = 11/3	q = 13/3
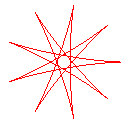
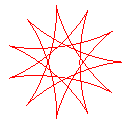
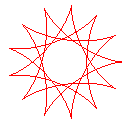
q = 9/4	q = 11/4	q = 13/4	q = 15/4	q = 17/4
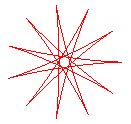
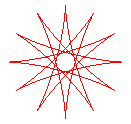
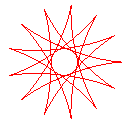
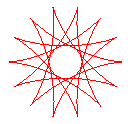
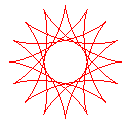
q = 11/5	q = 12/5	q = 13/5	q = 14/5	q = 16/5

L’hypocycloïde est l'enveloppe d'un diamètre d'un cercle de rayon double de celui de (C) roulant sans glisser sur et extérieurement à (C₀).

C'est aussi l'enveloppe d'une corde (PQ) du cercle de centre O et de rayon  (cercle des sommets de l'hypocycloïde), P et Q parcourant ce cercle dans des sens contraires et avec des vitesses constantes dans le rapport q – 1 (ceci constitue la génération dite de Cremona).
C’est enfin l’antipodaire par rapport à O de la rosace : .
Sa développée est sa propre image par la similitude directe de centre O, de rapport , et d’angle.

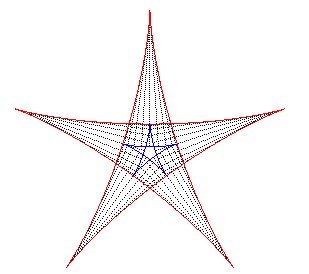
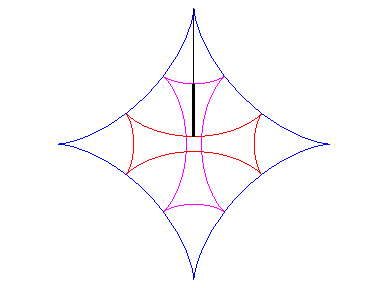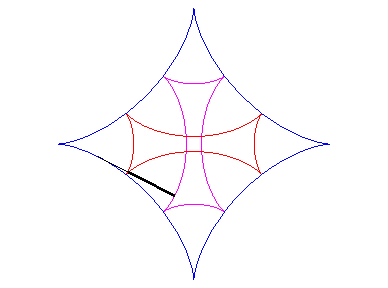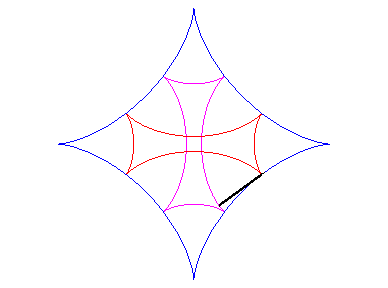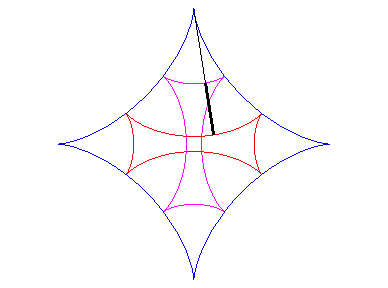
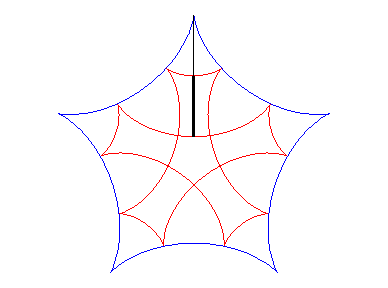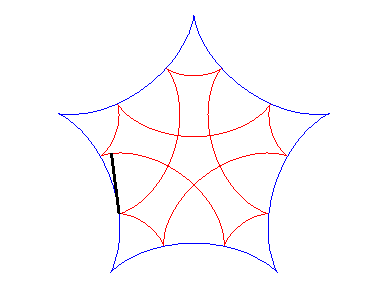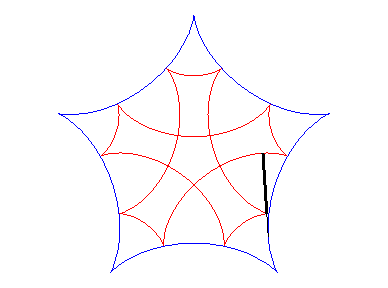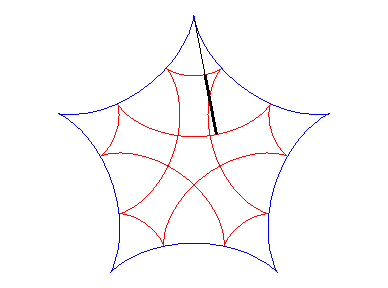
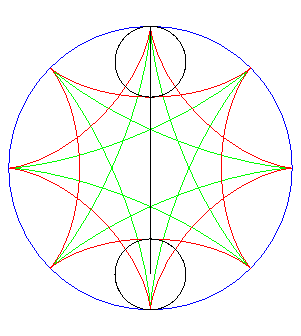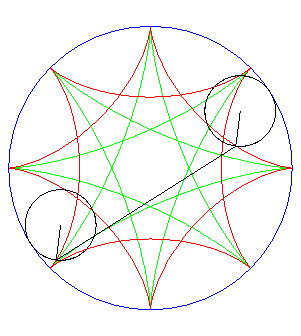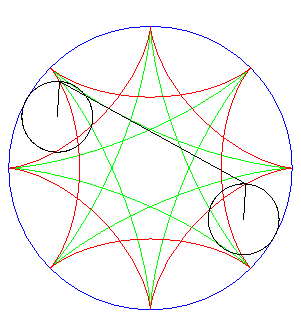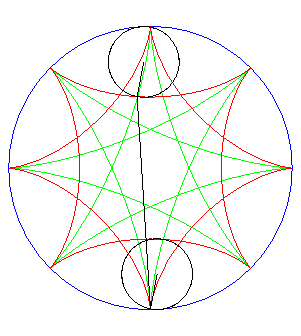
Si l'on fait rouler deux cercles traceurs symétiques par rapport au centre du cercle fixe mais en opposition de phase, le segment qui joint ces deux points (qui est de longueur constante) enveloppe une autre hypocycloïde, de paramètre  ; ci-contre, les cas q = 4 et 5 ; lorsque q = 3, q' = 3 (voir la remarquable construction et son application à deltoïde).
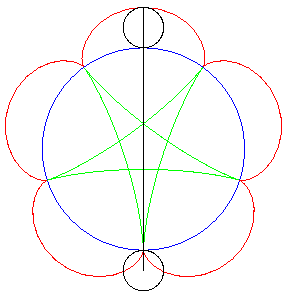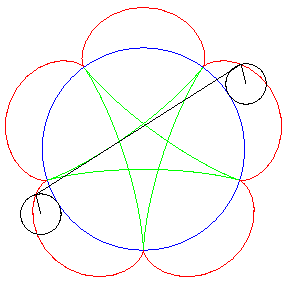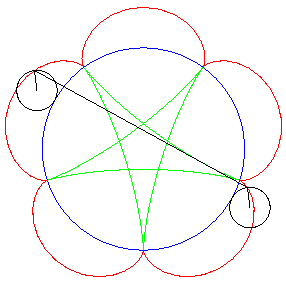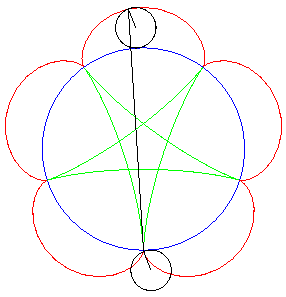
Idem si les cercles traceurs sont externes au cercle fixe ; les points P et Q traçant une épicycloïde de paramètre q, le segment PQ enveloppe de nouveau une hypocycloïde de paramètre  ; ci-contre, les cas q = 4 et 5 ; lorsque q = 3, q' = 3 (voir à deltoïde).

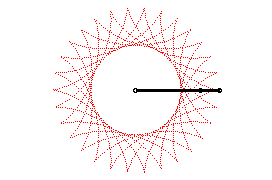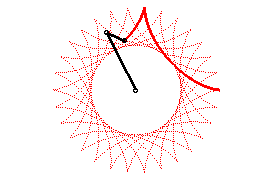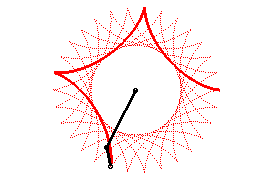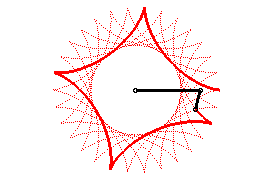
On peut aussi définir les hypocycloïdes comme les trajectoires d’un mouvement somme de deux mouvements circulaires uniformes de même vitesse et de sens contraires (de paramétrisation complexe : avec ).

Les hypocycloïdes sont aussi des projections d'hélices sphériques, et enfin, les courbes des petites oscillation du pendule de Foucault.

L'équation différentielle  montre, via l'équation d'Euler-Lagrange que, de même que la cycloïde, l'hypocycloïde est une courbe brachistochrone : c'est la courbe plane qui minimise le temps de parcours d'un mobile soumis à un champ de forces central en 1/r se déplaçant librement le long de cette courbe ; c'est donc la forme d'un tunnel creusé dans la terre qui minimiserait le temps de parcours d'un point A à un point B de la surface, par simple gravité.

Voir aussi en 3D les cycloïdes sphériques.
 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL, Jacques MANDONNET 2010