Équation fonctionnelle :  minimal (expression provenant du fait que la vitesse du mobile est proportionnelle à ). Équation différentielle (obtenue par application de l'équation d'Euler-Lagrange) : . Mouvement : , où , et où   est défini par . Temps de parcours :  où  est défini ci-dessus. Temps en ligne droite : . Temps par le chemin coudé : ().

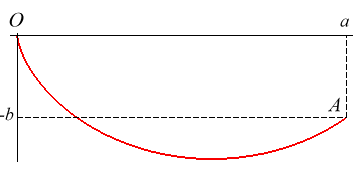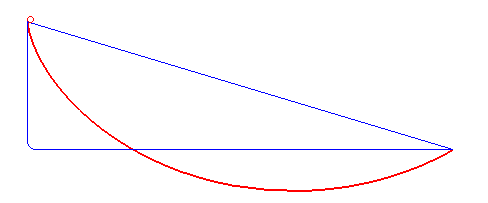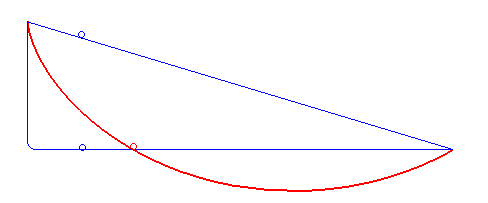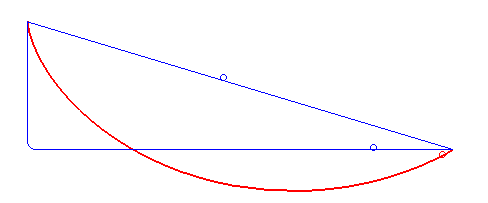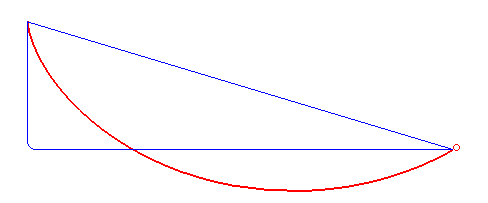
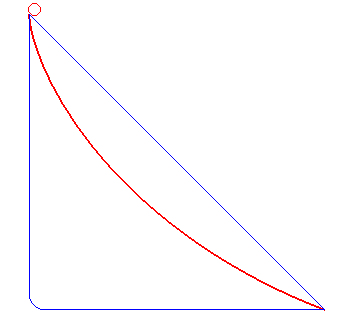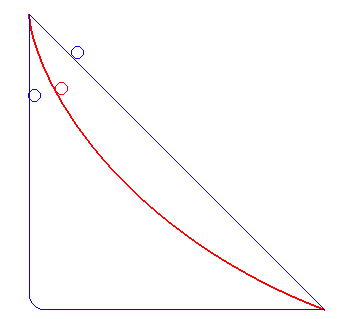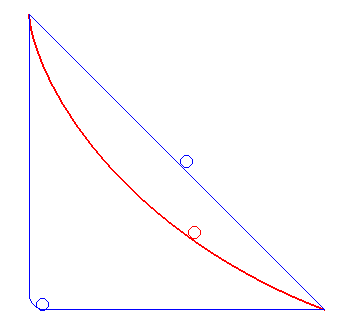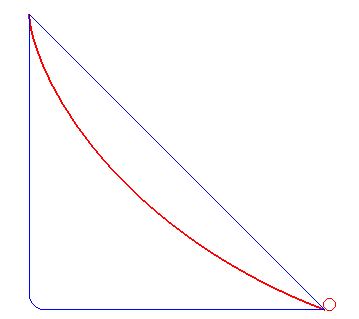
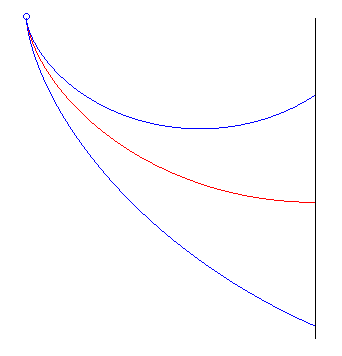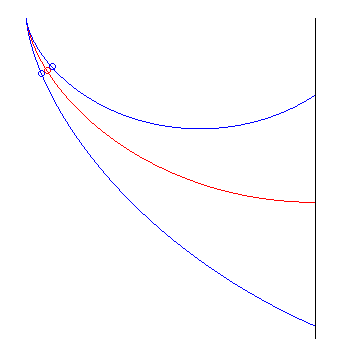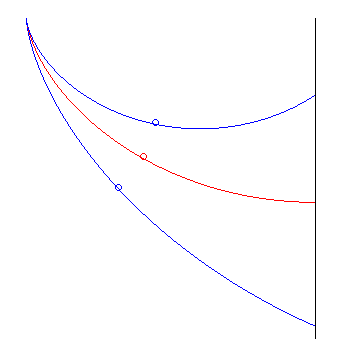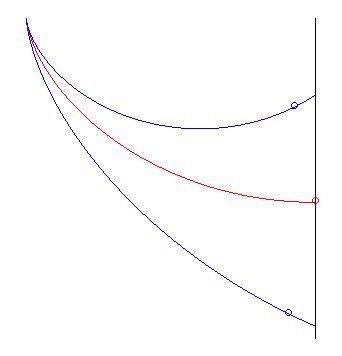
La (courbe) brachistochrone est la courbe sur laquelle doit glisser sans frottement et sans vitesse initiale, un point matériel pesant placé dans un champ de pesanteur uniforme de sorte que le temps de parcours soit minimal parmi toutes les courbes joignant deux points O et A fixés (ici A(a, –b)).

Réponse pour a > 0 (résultat trouvé en même temps par Leibniz, Newton, L'Hospital, Jean et Jacques Bernoulli) : un arc de cycloïde commençant avec une tangente verticale.

Il est remarquable que si la pente b/a entre O et A est inférieure à 2/p » 63%, correspondant à un angle de »32 ° avec l'horizontale, la courbe la plus rapide possède, comme dans la figure ci-dessus, une portion qui remonte !

Ceci vaut à la limite si les points O et A sont à la même altitude, auquel cas la ligne droite donnerait un temps de parcours infini.

Pour , on trouve un temps de descente     - de  pour la cycloïde,     - de  pour un arc de cercle (non représenté ci-contre),     - de   pour la ligne droite,     - de  pour une chute libre suivie d'un parcours horizontal (qui est donc battu par la ligne droite contrairement à ce qui se passe dans l'animation en haut de page).

 

Ici les deux boules sont côte à côte un moment, puis la bleue suit une ligne droite horizontale ; la cycloïde est toujours la plus rapide ! Animation dédiée à la rédaction des "incroyables expériences" de France 2 qui a du mal à accepter le phénomène...
Jean Bernoulli avait posé le problème sous une forme légèrement différente : trouver la courbe minimisant le temps de parcours en partant d'un point O à vitesse nulle et en arrivant à un plan vertical (en un point indéfini) : la réponse est une demi-arche de cycloïde à départ vertical et à arrivée horizontale et perpendiculaire au plan ;  à l'arrivée, le mobile sera donc descendu d'une hauteur égale à  fois la distance de O au plan.	la cycloïde rouge bat les deux autres
On peut aussi se demander quelle sera la courbe brachistochrone parmi les courbes reliant deux points donnés, et ayant une forme donnée. Par exemple pour deux points à même altitude et des courbes en V, la brachistochrone est celle dont l'angle du V est droit, comme le montre l'animation ci-contre. Cet exemple montre aussi que parmi tous les chemins rectilignes partant d'un point A donné et arrivant à un plan vertical P donné, le chemin brachistochrone est celui faisant un angle de 45° avec l'horizontale contenu dans le plan vertical passant par A et perpendiculaire à P (résultat obtenu par Galilée en 1638). Le problème de la brachistochrone de longueur donnée est traité sur cette page.
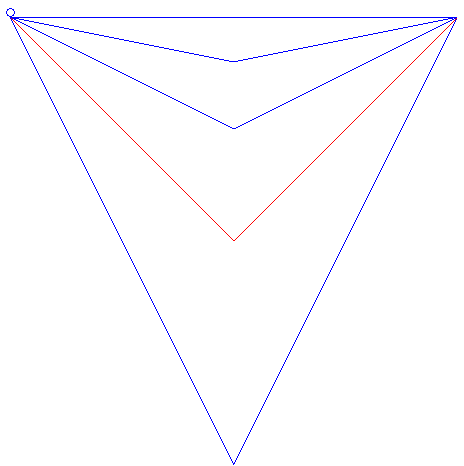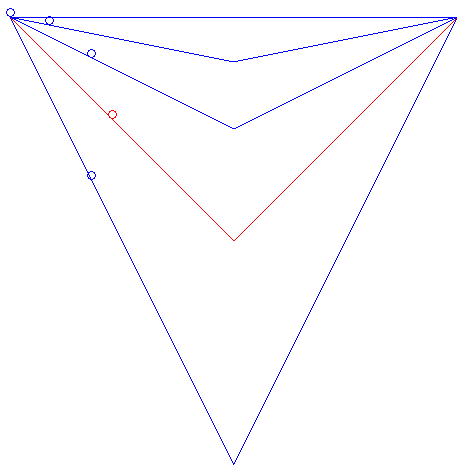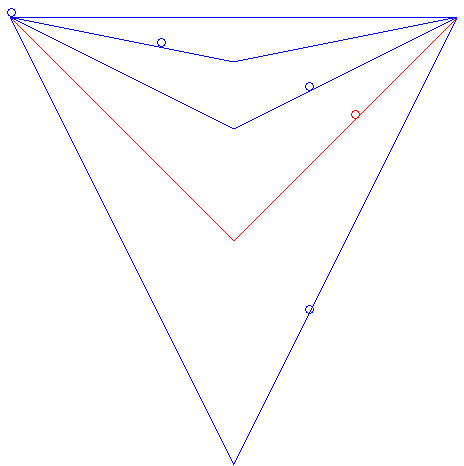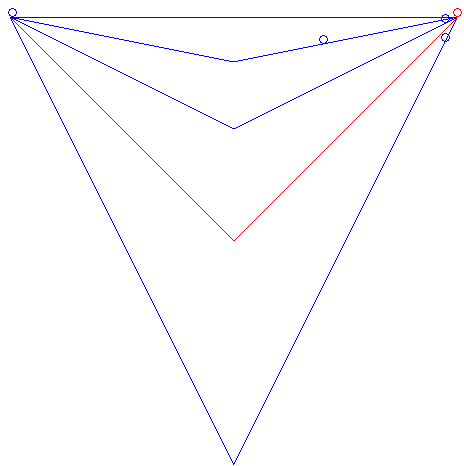On peut chercher aussi la brachistochrone "avec frottement" ; on obtient la paramétrisation  où  est le coefficient de frottement. Ci-contre, la brachistochrone sans frottement (donc la cycloïde) est en rouge. Voir cet article.

 

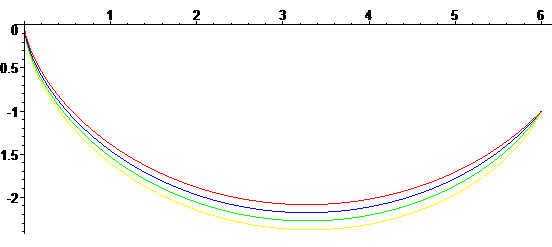Les concepteurs de rampes de skate savent-ils que la rampe la plus rapide a une forme de cycloïde ? La réponse est oui d'après l'article d'où sont tirés les graphiques ci-contre, mais apparemment, il n'y a pas eu de réalisation de rampe cycloïdale.

Généralisations :
On peut considérer des courbes brachistochrones tracées sur des surfaces.

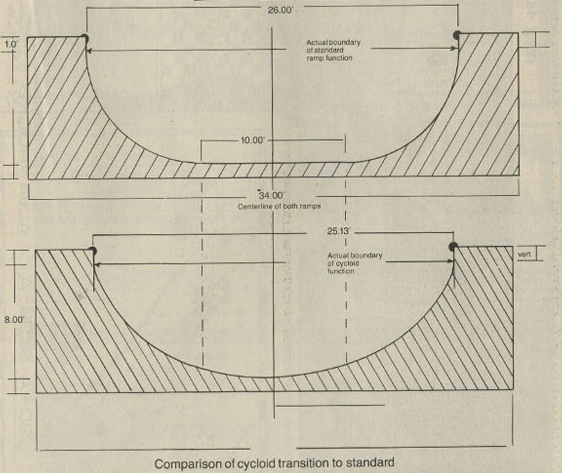On peut aussi chercher les courbes brachistochrones obtenues pour diverses lois de vitesse.
Ici , mais pour le cas plus général , la brachistochrone a pour équation différentielle .
Si , la brachistochrone obtenue est cette fois un arc de cercle.
Si maintenant la vitesse ne dépend que de la distance à O (), la brachistochrone a pour équation différentielle .
Pour , la brachistochrone est la spirale logarithmique ; ce cas correspond à un mobile situé dans un référentiel en rotation uniforme autour d'un point O (donc soumis à la force centrifuge), dans le cas où la vitesse est nulle en O.
 

Si la vitesse nulle est prise à une distance a de O , alors  ; la brachistochrone est alors une épicycloïde. Ceci peut avoir des applications sur la forme du chistera de la pelote basque, de sorte que la balle ait, à la sortie, la vitesse maximale. Le cas  est celui d'un mobile soumis à la gravitation terrestre (a étant le rayon de la terre), et a pour solution une hypocycloïde ; c'est donc la forme d'un tunnel creusé dans la terre qui minimiserait le temps de parcours d'un point à un autre de la surface, par simple gravité. Voir par exemple mathworld et ce texte.

En rouge, le tunnel brachistochrone.

Pour d'autres courbes de mouvement d'un point matériel dans un champ de pesanteur soumises à certaines conditions, voir à isochrone, tautochrone, synchrone, synodale, et courbe à réaction constante.
 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL, Jacques MANDONNET 2014