SPIRALE LOGARITHMIQUE
Equiangular
spiral, logarithmische Spirale
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
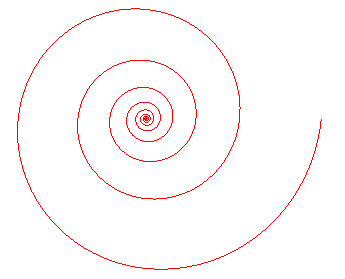
SPIRALE LOGARITHMIQUE
Equiangular
spiral, logarithmische Spirale

| Courbe étudiée par Descartes et Toricelli
en 1638, puis par Jacques Bernoulli (1654-1705).
Autres noms : spirale équiangle, spirale de Bernoulli, spira mirabilis ; le nom "spirale logarithmique" a été donné par Varignon. Jacques Bernoulli a fait graver une spirale logarithmique sur sa tombe dans la cathédrale de Bâle, avec l’épigraphe : eadem mutata resurgo, "déplacée (mutata), je réapparais (resurgo) à l'identique (eadem)". Cependant, le graveur a tracé une spirale d'Archimède... |
 |
 |
Équation polaire : Paramétrisation complexe : Courbe transcendante. Abscisse curviligne et équation intrinsèque 2 : Rayon de courbure : Équation intrinsèque 1 : Équation intrinsèque 2 : Équation podaire : |
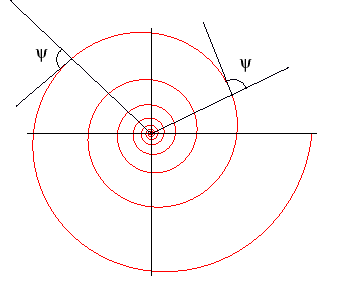
La spirale logarithmique peut être définie
comme
- courbe dont l'angle tangentiel polaire reste
constant (non droit)
- courbe dont la courbure est inversement
proportionnelle à l’abscisse curviligne
- courbe dont le rayon de courbure
est proportionnel (et supérieur) au rayon vecteur (
avec l > 1)
Les spirales logarithmiques de
centre O sont donc les trajectoires
sous l'angle.
du faisceau des droites issues de O.
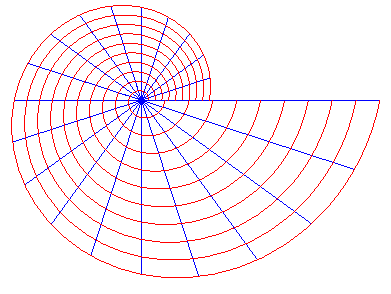
On peut aussi définir la spirale logarithmique de façon cinématique comme trajectoire d'un point M se déplaçant sur une droite passant par O avec une vitesse proportionnelle à OM, cette droite tournant elle-même uniformément autour de O ; ou encore comme courbe en coordonnées polaires telle que lorsque l'angle polaire croit de façon arithmétique, le rayon vecteur croit de façon géométrique.
La spirale logarithmique est aussi la projection stéréographique
de pôle sud des loxodromies
des sphères de centre O, faisant un angle
avec les méridiens (puisque la projection stéréographique
est une transformation conforme).
C'est enfin le développement plan d'une hélice d'un cône de révolution.
La spirale logarithmique présente une exceptionnelle stabilité vis à vis des transformations géométriques classiques :
- toute rotation de centre O
d’angle
de la spirale revient à une homothétie de même centre
et de rapport
,
laquelle revient donc à l’identité si
.
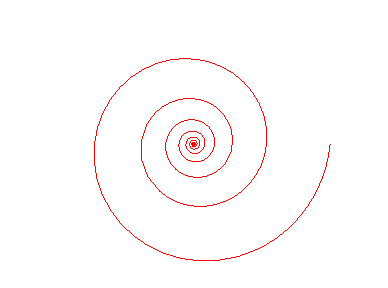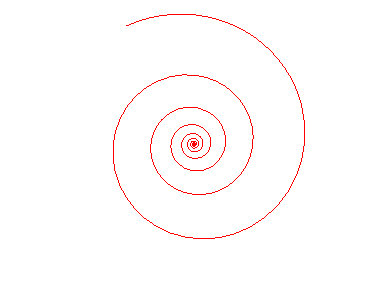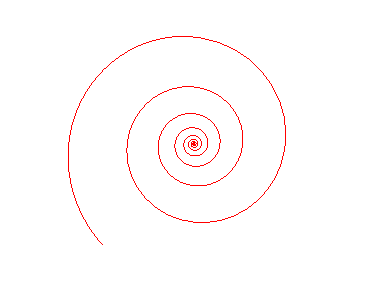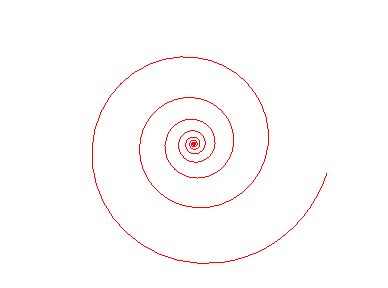
Rotation égale homothétie ! |
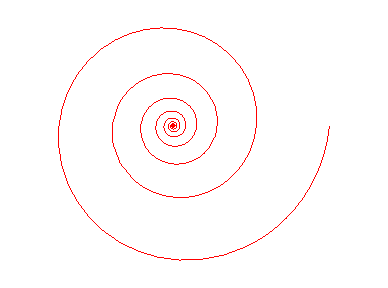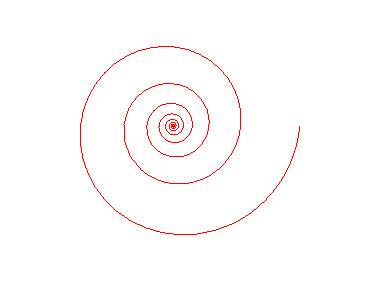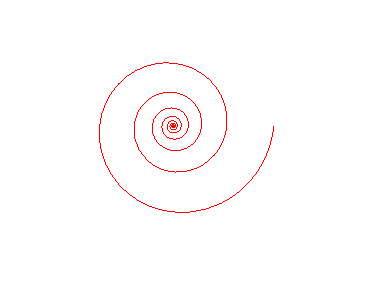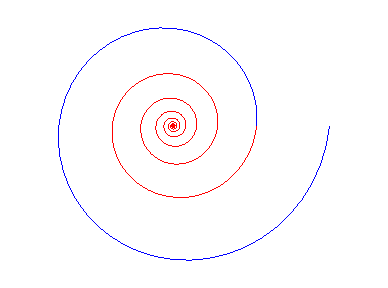
Homothétie égale identité ! |
- toute inversion de centre O
revient à une réflexion d'axe passant par O.
- sa développée
est une spirale logarithmique de même centre et de même angle (et
d'ailleurs la limite de la développée n-ième
de toute courbe est une spirale logarithmique).
- ses caustiques par réflexion ou par diffraction, la source lumineuse étant en O sont des spirales logarithmiques.
- l'engrenage conjugué d'un engrenage en spirale logarithmique est une spirale logarithmique isométrique.
- la barycentrique d'une spirale logarithmique est une spirale logarithmique isométrique.
Lorsqu'on fait rouler une spirale logarithmique sur une droite, le point asymptote décrit une autre droite :
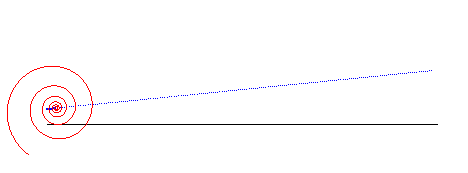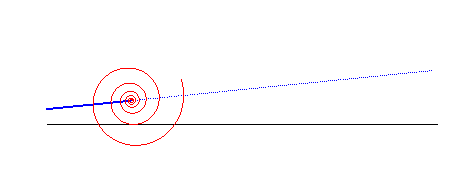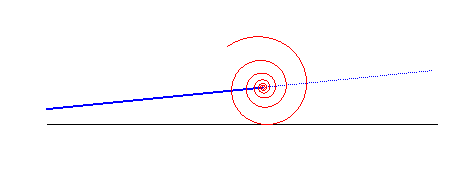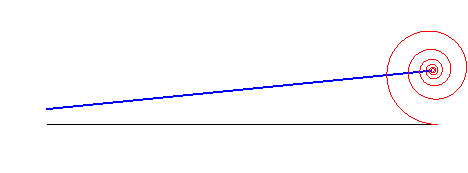
La spirale logarithmique est solution des trois problèmes de physique suivants :
1) La force centrée sur O
qui fait décrire à un point dans le vide une spirale logarithmique
est proportionnelle à 1/r3
(cette force est d'après la formule de Binet proportionnelle à
qui vaut ici
,
avec u = 1/r).
2) la courbe (dite brachistochrone)
qui minimise le temps de parcours d'un mobile se déplaçant
librement le long de cette courbe, cette courbe tournant à vitesse
constante autour d'un centre fixe O, dans le cas où le mobile
a une vitesse nulle lorsqu'il est en O, est une spirale lmogarithmique.
3) Le mouvement d’une particule de
masse m1 de charge q lancée
dans un champ magnétique uniforme d’intensité B avec
une vitesse v0 perpendiculaire au
champ est une spirale logarithmique avec
et
.
voir : perso.libertysurf.fr/hdehaan/mecanique/M6/M6_2/M6_2_cadre.htm
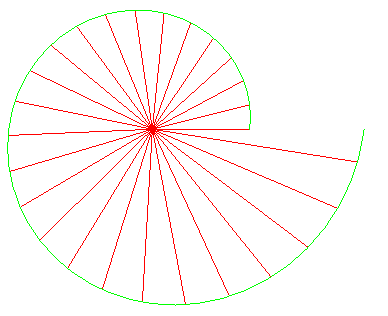
| Si u est un nombre complexe non nul, la suite
géométrique de raison u Ci-contre, avec u = 1+i/4. |
 |
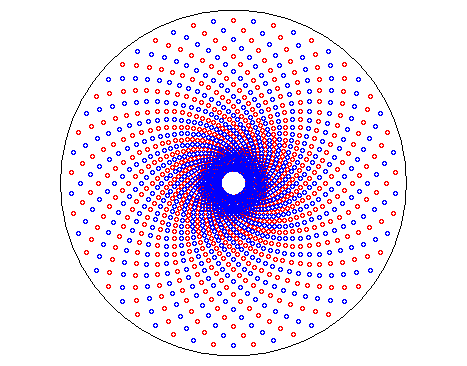
| De la même façon, toute suite de points
de coordonnées polaires Par exemple, sur la figure ci-contre ont été
tracés les points de coordonnées polaires ((1,1)k
; (k+2l)p/n), en bleu si
l
est pair, en rouge sinon ; ces points sont situés en quinconces
à l'intersection de cercles concentriques de rayons en progression
géométrique et de droites concourantes ; mais ils sont aussi
situés sur les spirales logarithmiques d'équation |
|
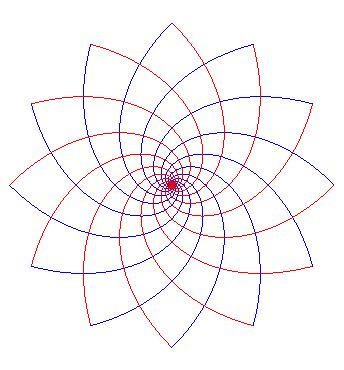
 |
Ici, les mêmes spirales, mais coloriées en triangles à la manière de cette mosaïque qui ornait une villa romaine à Corinthe au 2ème siècle après J.C. |  |
| D'autre part, comme on le constatait sur les figures
précédentes, les spirales |
 |
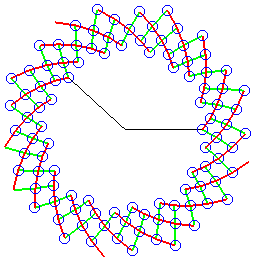
| Phyllotaxie
Les écailles des pommes
de pin se développent suivant une spirale logarithmique telle
que l'écart angulaire (par rapport au centre) entre deux écailles
successives, est à peu près égal à l'angle
d'or : |
 |
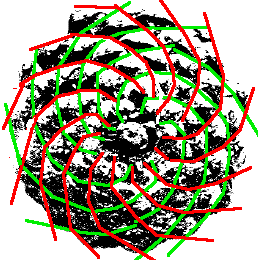 |
| Vue des points de coordonnées polaires On voit apparaître Sur la figure où les écailles sont indiquées avec leur numéro d'apparition, on remarque que la k-ième spirale secondaire associée à Les écailles de la k-ième spirale secondaire associée à Nota : l'angle entre deux spirales rouge et verte qui
se croisent est constant mais n'est pas lié à l'angle d'or
comme on le voit parfois écrit, puisqu'il dépend de la valeur
de r !
|
 |
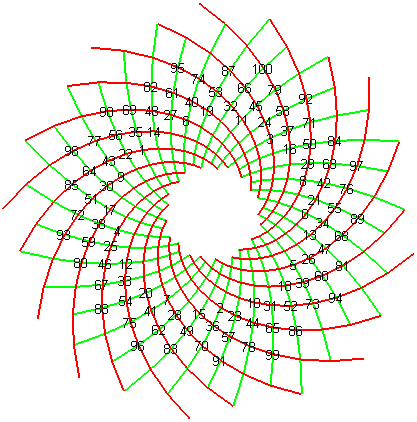 |
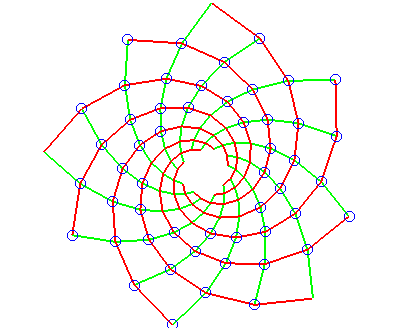
| Si l'on augmente le rapport r à 1,02, ce
sont plutôt les 8 = Ces spirales secondaires associées aux nombres de Fibonacci apparaissent visuellement car les multiples fibonacciens de l'angle d'or se rapprochent de l'angle nul (voir wikipedia) : on voit bien sur la figure où les écailles sont indiquées avec leur numéro d'apparition que les écailles fibonacciennes 3, 5, 8, 13, 21, 34, 55, 89 se rapprochent de l'axe des x. Voir par exemple ce site ou celui-ci pour d'autres explications. Sur cette page, on pourra tester différents angles de rotation entre deux fleurons de tournesol et constater que la disposition des fleurons est optimale dans le cas de l'angle d'or. |
 |
 |
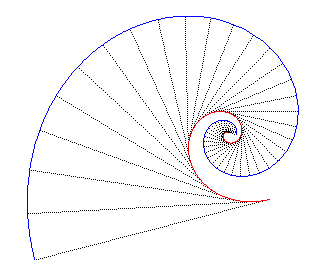
Si l'on considère une suite de droites concourantes
D1,
D2,
.... faisant chacune un angle
e avec
la suivante, et que, partant de M1
sur D1, on construit M2
sur D2 tel que l'angle entre D1
et M1M2
soit égal à ,
puis M3,
M4,
... de la même façon, les points Mn
ont des modules en progression géométrique de raison
et des arguments en progression arithmétique de raison e,
de sorte qu'ils se trouvent sur une spirale logarithmique avec
; on vérifie que
tend bien vers cot
quand
tend vers 0, de sorte que la spirale correspondant à
tend
vers la spirale logarithmique avec k = cot
.
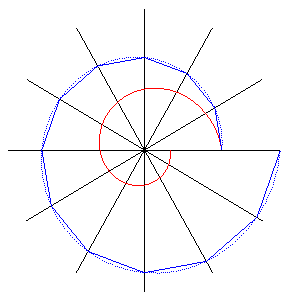
ici, y = 100°, e = p/10. |
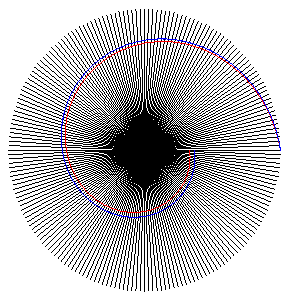
ici, y = 100°, e = p/50. |
REM : lorsque
= 90°, on construit Mi+1
comme ayant Mi
pour projeté orthogonal sur Di
(attention, ne pas confondre avec la spirale
de Théodore qui est une spirale
d'Archimède approchée).
Une autre construction approchée consiste à
prendre des arcs de cercle d'angles constants et
de rayons en progression géométrique de raison
,
raccordés tangents.
Pour un très beau cas particulier, voir à
spirale
d'or. La spirale tracée sur un cône qui se projette en
une spirale logarithmique est l'hélice
conique.
Voir aussi la spirale de la tige en rotation et les courbes de poursuite mutuelle.

Plafond d'une salle du château de Pavlovsk à Saint Pétersbourg
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2019