Courbe logarithmique

LOGARITHMIQUE (COURBE)
Logarithmic curve, Logarithmuskurve

Autre nom : courbe exponentielle.

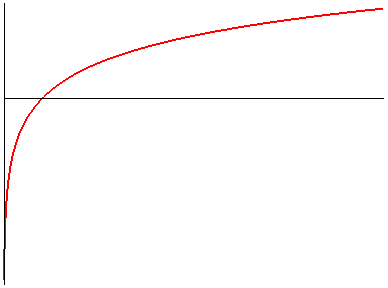
Version logarithmique :
Équation cartésienne : .
Courbe transcendante.
Dans le cas a = b :
Abscisse curviligne en partant du point d'abscisse a :

L'angle tangentiel cartésien est défini par .
Rayon de courbure : .

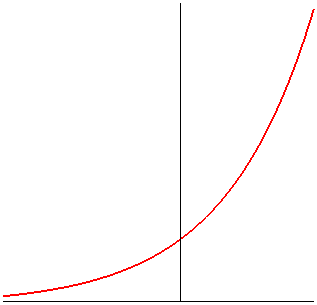
Version exponentielle :
Équation cartésienne : .
Courbe transcendante.
Dans le cas a = b :
Abscisse curviligne en partant du point d'abscisse 0 :
.
L'angle tangentiel cartésien est défini par .
Rayon de courbure : .

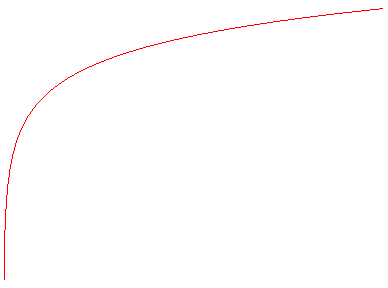
La logarithmique est la courbe de la fonction logarithme (et aussi celle de la fonction exponentielle) ou son image par une dilatation.

CNS : courbe dont la sous-tangente est constante.

La logarithmique est aussi caractérisée par le fait que sa translation le long de son asymptote équivaut à une dilatation perpendiculairement à cette asymptote.
Translation équivaut à affinité

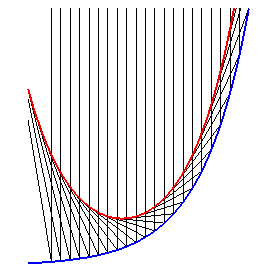
Dans le cas a = b, sa caustique par réflexion pour des rayons perpendiculaires à son asymptote est la chaînette.
Pour des rayons parallèles à l'asymptote, c'est une courbe de poursuite.

La logarithmique est le profil qu'il faut donner à une tour (c'est-à dire un solide de révolution) pour que la pression exercée sur toute section horizontale par la partie supérieure soit constante.
Voir à tour à pression constante.

Voir aussi la développante d'exponentielle, la parabole amortie, la chaînette et la tractrice.

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres

Version logarithmique : Équation cartésienne : . Courbe transcendante. Dans le cas a = b : Abscisse curviligne en partant du point d'abscisse a : L'angle tangentiel cartésien est défini par . Rayon de courbure : .
Version exponentielle : Équation cartésienne : . Courbe transcendante. Dans le cas a = b : Abscisse curviligne en partant du point d'abscisse 0 : . L'angle tangentiel cartésien est défini par . Rayon de courbure : .