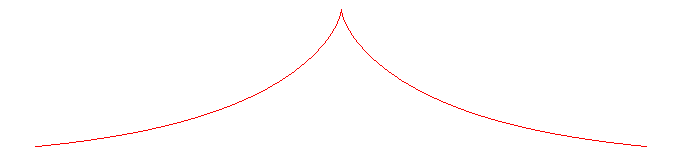
Tractrice

TRACTRICE
Tractrix, Traktrix

Courbe considérée par Claude Perrault en 1670, puis étudiée par Newton en 1676, Huygens en 1692 et Leibniz en 1693.
Autre nom : courbe équitangentielle (car la tangente:T y est constante)

Équation différentielle :

, soit

.
Paramétrisation cartésienne :

où

(gd est la fonction de Gudermann).
Ou encore

.
Équation cartésienne :

.
Courbe transcendante.
Abscisse curviligne (pour la première paramétrisation) :

. Angle tangentiel cartésien :

.
Rayon de courbure :

.
Équation intrinsèque 1 :

. Équation intrinsèque 2 :

.
Aire entre la courbe et l'asymptote :

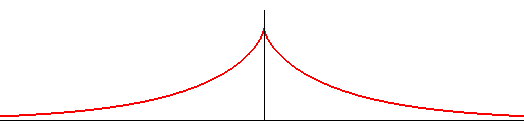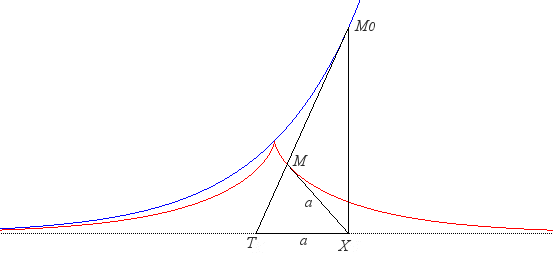
(aire du demi cercle de centre O passant par le point de rebroussement ; voir ici une belle animation de ce fait).

La tractrice peut être définie comme tractoire de la droite, ou ce qui revient au même, comme courbe à tangente constante.

Le problème initial posé par Claude Perrault était de trouver la trajectoire d'une montre attachée à un chaînette dont l'extrémité décrit le bord d'une table.
De nos jour l'image serait plutôt celle de la trajectoire des roues arrière d'un véhicule dont les roues avant décrivent une droite.

La tractice est aussi :

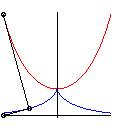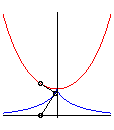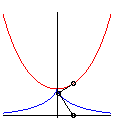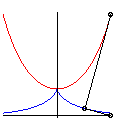
- la développante principale de la chaînette (i. e. développante dont le point de rebroussement est au sommet de la chaînette) ; ici, la chaînette a pour équation .

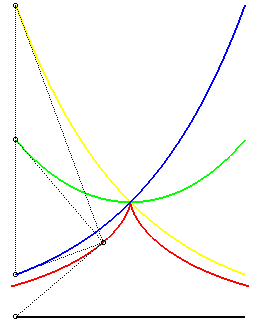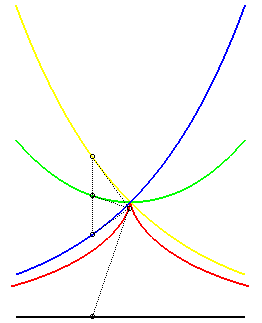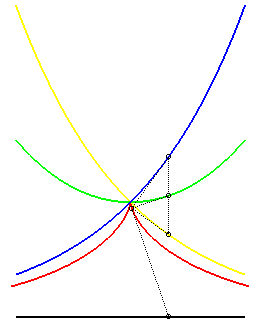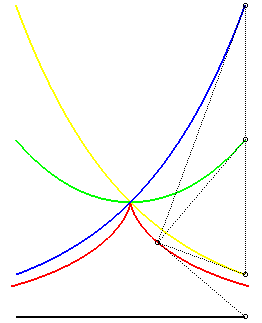
- le lieu des points d'où l'on peut mener une tangente à la logarithmique : et une tangente à la logarithmique symétrique : , qui soient orthogonales. Autrement dit, la tractrice est l'orthoptique de la réunion de ces deux logarithmiques.
Ci-contre, en bleu et jaune, les 2 logarithmiques, en rouge la tractrice correspondante, et en vert la chaînette médiane des deux logarithmiques.

- le lieu du point M construit comme suit : le point M0 décrivant la logarithmique , soit X le projeté sur Ox et T l'intersection de la tangente avec Ox. On sait que la "sous-tangente" TX est constante égale à a. le point M est le point de [M0T] tel que MX= a ; la droite (MX) enveloppe alors la tractrice.
(construction dûe à Pietro Milici, liée à la précédente).

- le lieu du centre d'une spirale hyperbolique roulant sans glisser sur une droite (c'est donc une roulette).

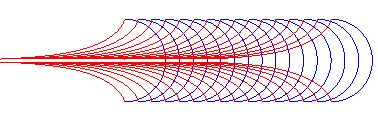
D'autre part, les trajectoires orthogonales de la famille des cercles centrés sur Ox de rayon a sont des tractrices translatées les unes des autres.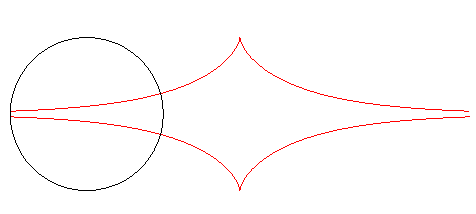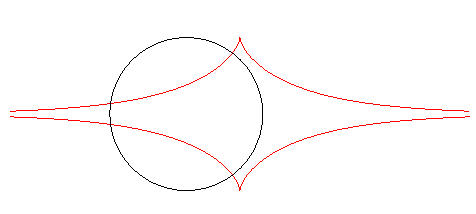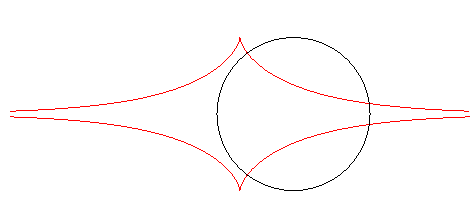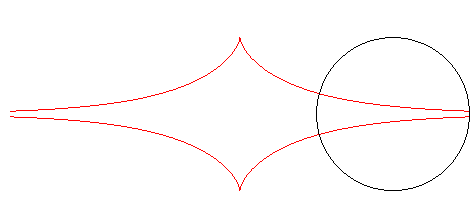

La podaire de la tractrice par rapport à O est l'élégante courbe de paramétrisation
ressemblant au bifolium régulier.

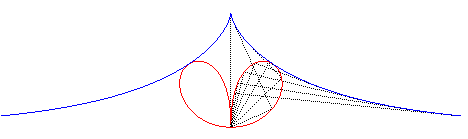La radiale de la tractrice est le kappa.
Sa rotation autour de la base engendre la pseudo-sphère.

Voir aussi les syntractrices et la développante sommitale de parabole.

Remarque : les courbes à normale constante ne sont autres que les cercles.

Instrument dû à Perks permettant de tracer la tractrice.

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres

- la développante principale de la chaînette (i. e. développante dont le point de rebroussement est au sommet de la chaînette) ; ici, la chaînette a pour équation .
- le lieu des points d'où l'on peut mener une tangente à la logarithmique : et une tangente à la logarithmique symétrique : , qui soient orthogonales. Autrement dit, la tractrice est l'orthoptique de la réunion de ces deux logarithmiques. Ci-contre, en bleu et jaune, les 2 logarithmiques, en rouge la tractrice correspondante, et en vert la chaînette médiane des deux logarithmiques.
- le lieu du point M construit comme suit : le point M0 décrivant la logarithmique , soit X le projeté sur Ox et T l'intersection de la tangente avec Ox. On sait que la "sous-tangente" TX est constante égale à a. le point M est le point de [M0T] tel que MX= a ; la droite (MX) enveloppe alors la tractrice. (construction dûe à Pietro Milici, liée à la précédente).
- le lieu du centre d'une spirale hyperbolique roulant sans glisser sur une droite (c'est donc une roulette).