Autres nom : rosace à quatre pétales/branches/feuilles/lobes, quadrifolium.

 

Équation polaire : . Equation cartésienne : . Sextique rationnelle Paramétrisation cartésienne dans un repère tourné de  : . Longueur : . Aire :  (moitié de celle du disque circonscrit ; les pétales "négatifs" découpés sur ce disque ont donc même aire que les "positifs")

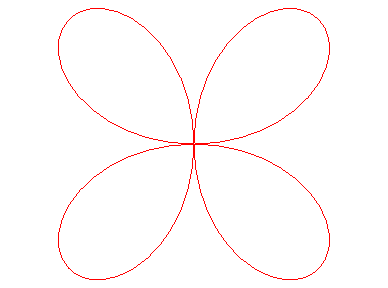
Le trèfle à quatre feuilles est la rosace à quatre pétales.

On peut l'obtenir comme trajectoire du deuxième point d'intersection d'une droite et d'un cercle tournant autour d'un de leurs points, soit dans le même sens le cercle tournant à une vitesse triple de la droite, soit en sens contraire avec la même vitesse.
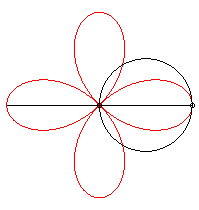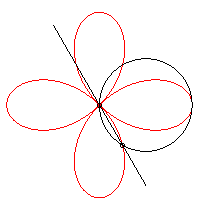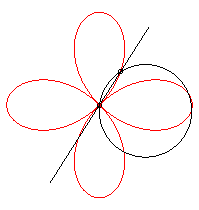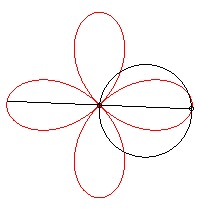
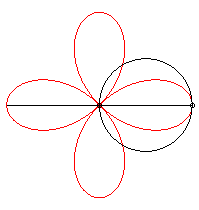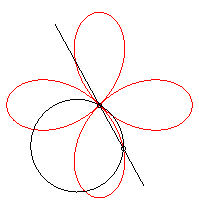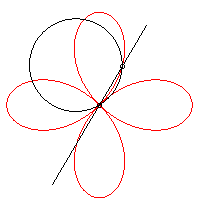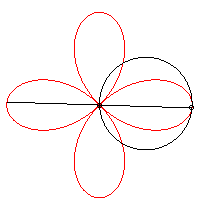
On  l'obtient aussi comme trajectoire du deuxième point d'intersection de deux cercles identiques tornant autour d'un de leurs points, en sens contraire l'un tournant à une vitesse triple de l'autre :

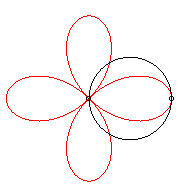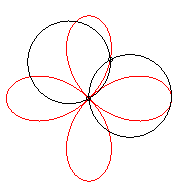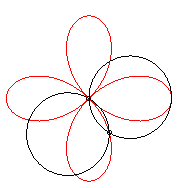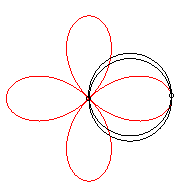Le trèfle à quatre feuilles est également :
 

- le lieu des pieds des perpendiculaires issues de O sur un segment de longueur 2a dont les extrémités se déplacent sur les axes ; c’est donc la podaire par rapport à O de l’astroïde : (le trèfle à quatre feuilles est donc une scarabée), ainsi que l'enveloppe des cercles dont un diamètre joint O à un point de cette astroïde.
- l'orthoptique de l'astroïde
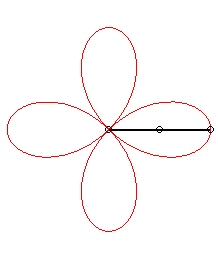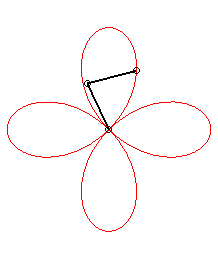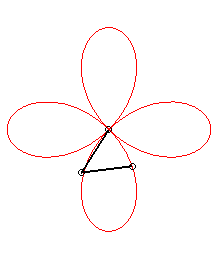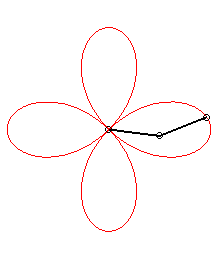
- une hypotrochoïde : somme de deux mouvements circulaires de même rayon, de sens contraires, les vitesses angulaires étant dans le rapport 3 ;  ou bien cercle de roulement de rayon , cercle roulant de rayon , distance du point au cercle roulant = .	quand le premier bras fait 1 tour, le deuxième en fait 3.

Il s'obtient aussi comme orthopolaire de cercle.
 

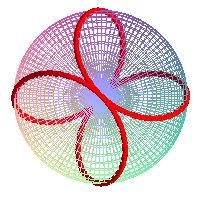
Comme pour toute rosace, le quadrifolium est la vue de dessus d'une clélie. Cette élégante courbe sphérique d'équation cylindrique  est ici un cas limite de la couture de la balle de tennis.

Le quadrifolium s'obtient aussi par projections à partir d'une couronne sinusoïdale à 2 arches (ou courbe de la crêpe), par l'intermédiaire d'une vasque 3D.

 

Ci-contre, quadrifoliums homothétiques (en rouge), et leurs trajectoires orthogonales.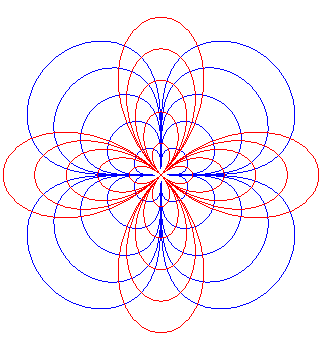

Voici quelques variantes donnant des trèfles à 4 feuilles un peu plus réalistes :
 

Réunion de deux  lemniscates de Bernoulli

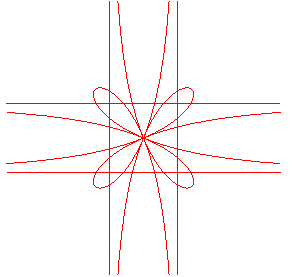
Deux quadrifolium à asymptotes : , soit (décique),  et , soit  (octique).

Voir aussi à trisectrice de Céva, à oeuf double (conchoïde de quadrifolium), à rosace conique, et à surface d'Enneper.
 
 

Superbe quadrifolium exécuté par un jongleur de bolas.

Trois boucles de quadrifolium situées dans 3 plans orthogonaux forment le bord d'une hélice à trois pales, qui se projette en un (faux) trifolium régulier... Voir aussi la courbe d'auto-intersection de la surface de Boy.

 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2011