OEUF DOUBLE
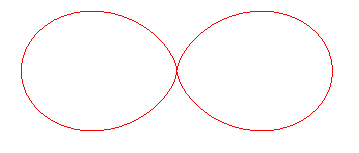
Double
egg curve, Doppeleikurve (od. Doppeleilinie)
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
OEUF DOUBLE
Double
egg curve, Doppeleikurve (od. Doppeleilinie)

| Courbe étudiée par Villalpando en 1606,
et par Münger en 1894.
Autres noms : biovale, courbe proportionnatrice (nom donné par Villalpando). |
| Équation polaire : Équation cartésienne : Abscisse curviligne : Rayon de courbure : Longueur d'un oeuf : Aire d'un oeuf : Sextique rationnelle. |
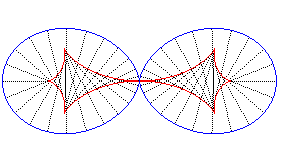
Oeuf double et sa développée ; la courbure est infinie au centre. |
L'oeuf double est la courbe
de Clairaut d'équation polaire ci-dessus, équation montrant
que c'est une
conchoïde du
trêfle
à 4 feuilles.
| C'est aussi l'inverse de la campyle d'Eudoxe par rapport à son centre : | 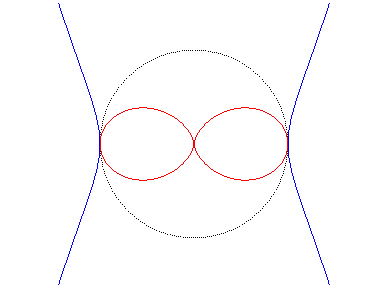 |
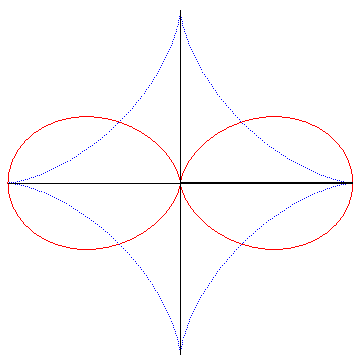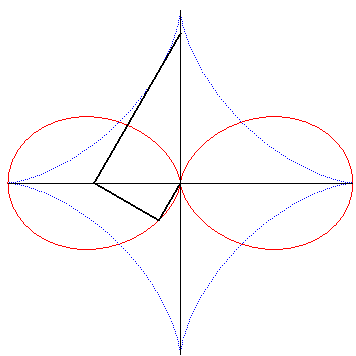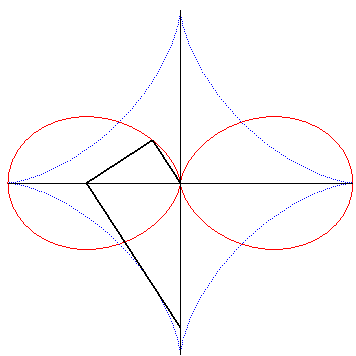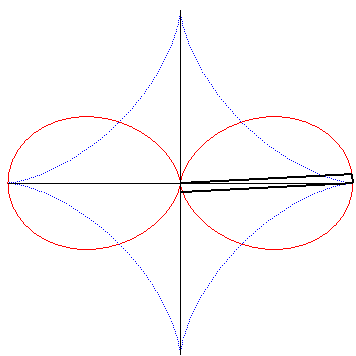
| Et on l'obtient par la construction suivante : un segment de longueur constante étant contraint de se mouvoir de sorte que ses extrémités se déplacent sur deux droites perpendiculaires sécantes en O, le projeté de O sur une perpendiculaire au segment en l'une de ses extrémités décrit un oeuf double. |
 |
| L'oeuf double est la glissette de la pointe d'une d'une cardioïde astreinte à être tangente à une droite fixe en un point fixe. |
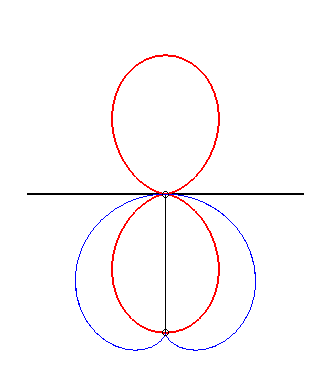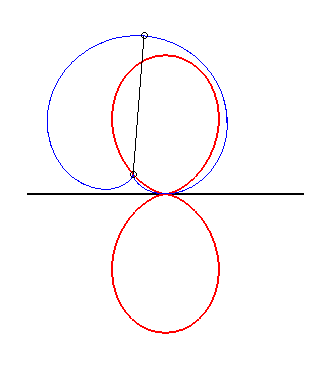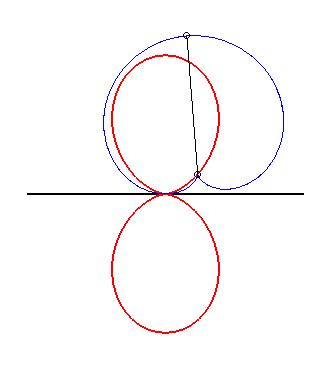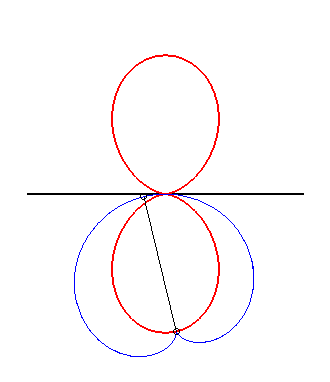 |
| Il s'obtient aussi par roulement d'une ellipse sur un quadrifolium. |
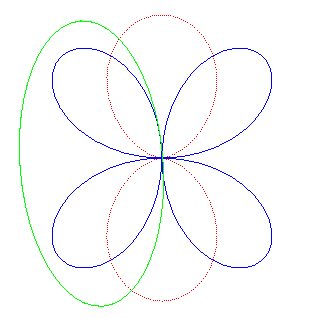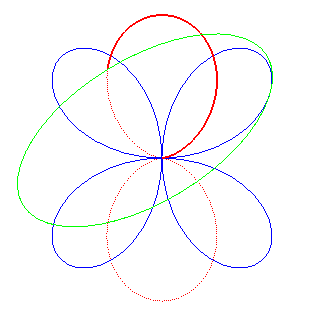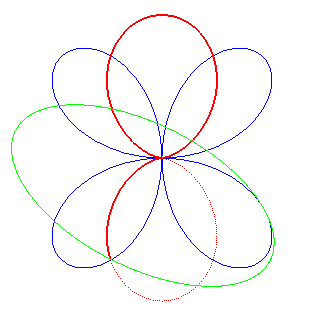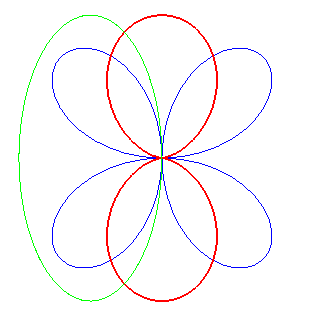 |
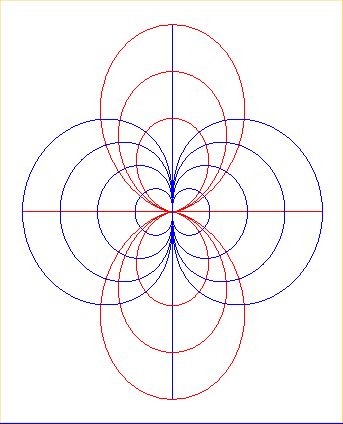
| Les lignes
de champ magnétique créées par un dipôle magnétique
sont des oeufs-doubles ; les lignes orthogonales sont alors les courbes
d'équations polaire |
 |
| La route nécessaire pour faire rouler une roue en forme d'oeuf double de sorte que le centre ait un mouvement rectiligne est une cycloïde ayant subi une affinité de rapport 1/2 (animation due à Alain Esculier) |  |
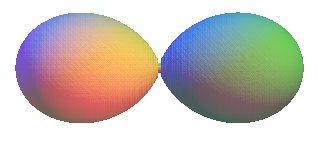
| La rotation autour de l'axe de symétrie coupant
les oeufs en deux donne une surface
de révolution d'équation |
 |
Comparer avec le folium
simple (
au lieu de
)
et regarder d'autres oeufs à ovoïde.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2016