Du grec Kampulos : courbé (qui a donné aussi le mot "jambe") Eudoxe de Cnide (406-355 avant J.C.) : astronome, mathématicien et philosophe grec. Autre nom : courbe de Clairaut.

 

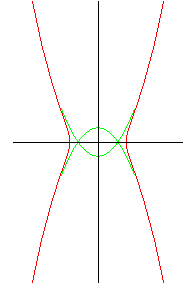Équation polaire :  (courbe de Clairaut). Équation cartésienne :  ou  . (à comparer avec celle de la lemniscate de Gerono). Quartique rationnelle. Equation des paraboles asymptotes (en vert) : .

 

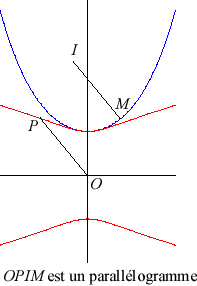
Un point P parcourant un cercle (C) de centre O, la tangente à (C) en P coupe Ox en Q ; la campyle d'Eudoxe est le lieu du point d'intersection de la droite (OP) et de la parallèle à Oy passant par Q.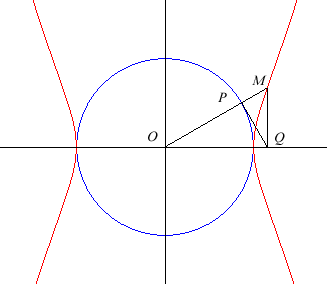

 

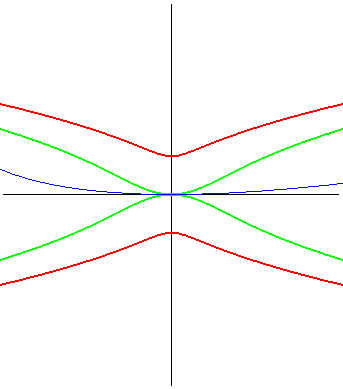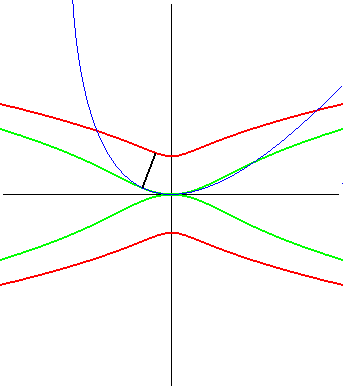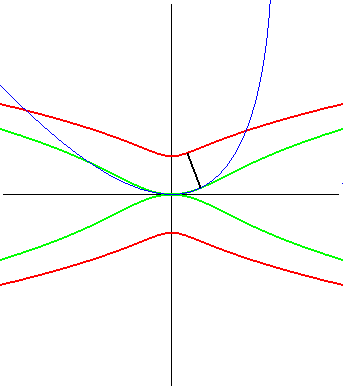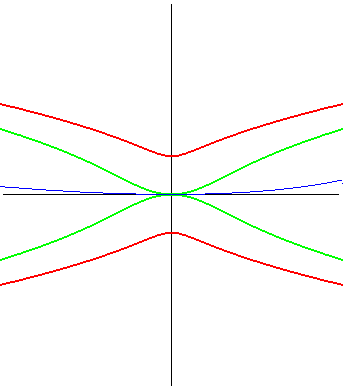
La kampyle (en rouge ci-contre) est aussi le lieu du foyer d'une parabole astreinte à rester tangente à une droite en un point fixe ; c'est donc une glissette. Pour une parabole de paramètre p, on obtient une kampyle de paramètre a = p/2.
L'intersection d'un tore à trou nul avec un cône de révolution de sommet le centre du tore est une courbe dont la projection sur le plan du cercle central du tore est une portion de kampyle. Par exemple, l'intersection du tore à trou nul de rayon a :  avec le cône de révolution droit :  est la courbe de système d'équations cartésiennes : , qui se projette sur xOy en la portion de kampyle :  (voir cette page du mathouriste).
La kampyle d’Eudoxe est aussi la radiale de la chaînette (ici, modulo une rotation d'angle p/2),
ainsi que l'inverse de l'oeuf double,

et également un cas particulier de polygastéroïde.

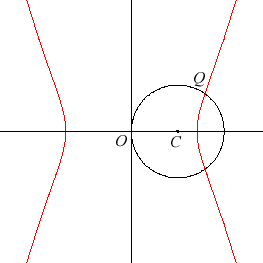
Elle a été considérée par Eudoxe car c'est une duplicatrice ; en effet, si on la coupe avec le cercle de centre C passant par O (d'équation  ), le point d'intersection Q est à la distance   de O.

On retrouve aussi la kampyle comme roulante du mouvement conchoïdal rectiligne, et comme base du mouvement du kappa (voir cette page).
 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2023