Courbe étudiée par Rømer en 1674, Vaumesle en 1678, La Hire en 1708 et Castillon en 1741. Le nom, donné par Castillon en 1741, provient du grec kardia "coeur".

 

Équation polaire :  Équation cartésienne :. Quartique bicirculaire rationnelle. Paramétrisation cartésienne : (où ). Paramétrisation cartésienne rationnelle : . Paramétrisation complexe : (où ). Angles tangentiels polaire, cartésien : ,. Abscisse curviligne :  Rayon podaire : .  Rayon de courbure :  Équation intrinsèque 1 :  Équation intrinsèque 2 : (ici, cte= -) Équation podaire :  Longueur : 8a ; aire : 3pa2/2.

La cardioïde dispute à la lemniscate de Bernoulli le record du nombre d'appartenances aux diverses familles de courbes remarquables ; la cardioïde est en effet :

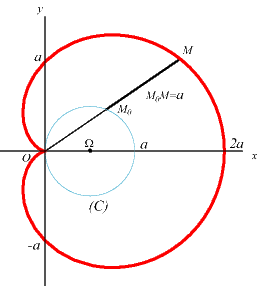
1) une conchoïde de cercle relativement à un point situé sur le cercle, avec un module égal au diamètre du cercle. Pour obtenir l’équation indiquée en en-tête, prendre la conchoïde du cercle (C) de centre W (a/2, 0) passant par O, relativement à O, de module a (la cardioïde est donc un cas particulier de limaçon de Pascal).
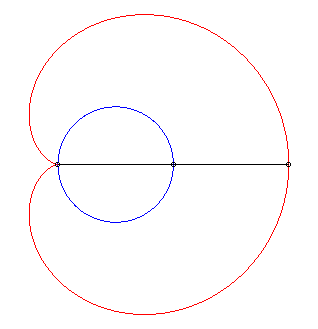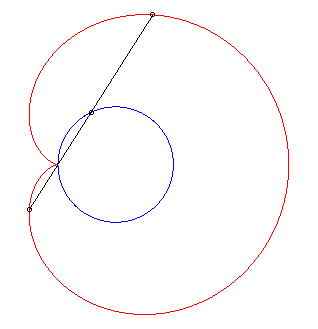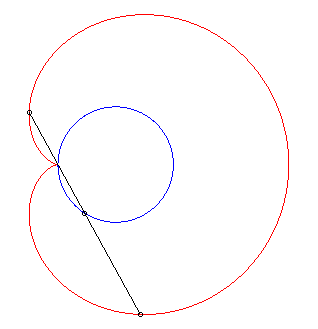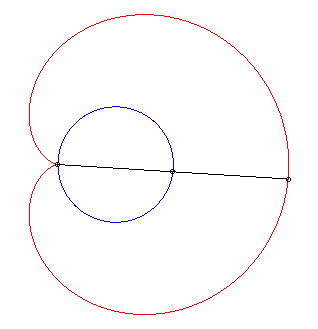
D'où la construction mécanique ci-dessous à partir d'un bâton de longueur 2a coulissant par un point fixe de (C) et dont le centre est contraint de décrire (C).
 

2. a) une épicycloïde à un rebroussement : lieu d'un point d'un cercle roulant sans glisser, extérieurement, autour d’un cercle de même rayon (ici, cercle de rayon a/2 roulant sans glisser autour du cercle (C) ). Notons que le cercle roulant tourne deux fois sur lui-même lorsqu'il revient à son point de départ.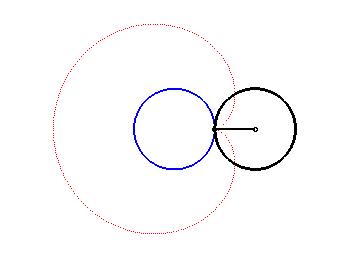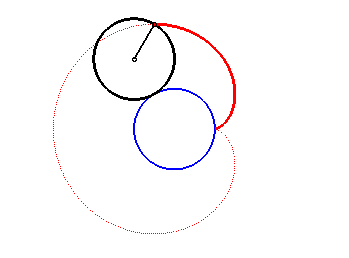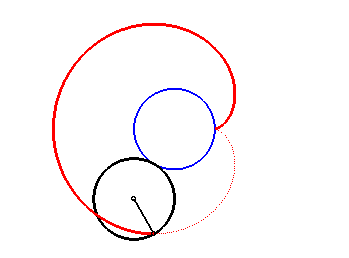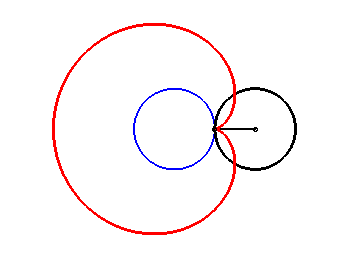

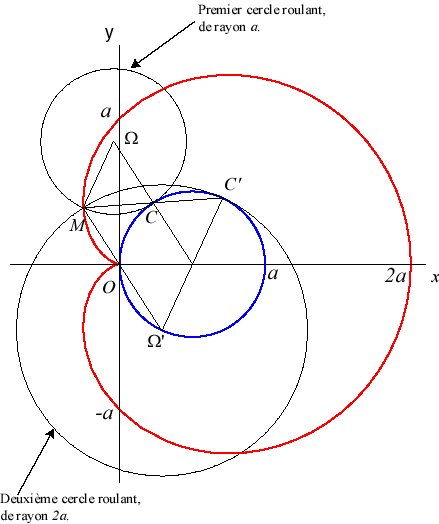
C’est donc aussi :
    b) la courbe orthotomique d'un cercle par rapport à l'un de ses points.
    c) une péricycloïde ((cercle roulant sans glisser autour d’un cercle de rayon moitié en le contenant ; ici, cercle de rayon a roulant autour de (C)).
 

    d) l'enveloppe d'un diamètre d'un cercle de rayon a roulant sans glisser sur et extérieurement à (C₀).
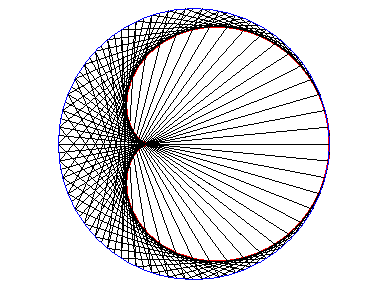
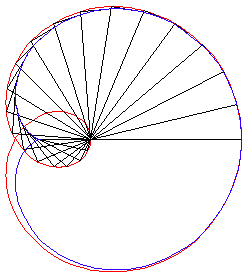
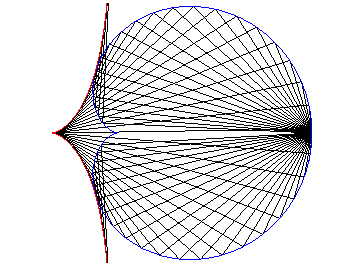
    e) l'enveloppe d'une corde (PQ) du cercle de centre W et de rayon (cercle circonscrit à la cardioïde), P et Q parcourant ce cercle dans le même sens, l’un ayant une vitesse double de l’autre (génération dite "de Cremona").

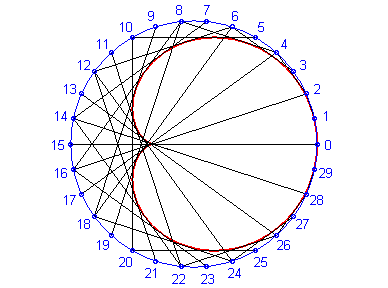
Ci-dessus, le point n est relié au point 2n modulo 30.

3) comme toute quartique bicirculaire rationnelle :
    3. a) une podaire de cercle par rapport à l’un de ses points ; ici, la podaire du cercle (C') de centre (a, 0) passant par O, par rapport à O ((C') est le cercle inscrit dans la cardioïde).

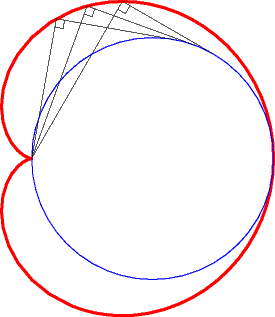
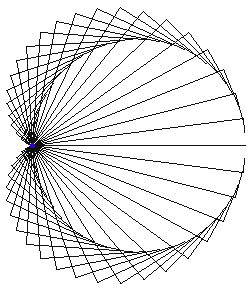
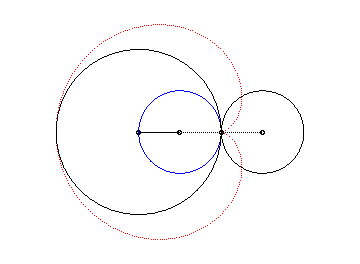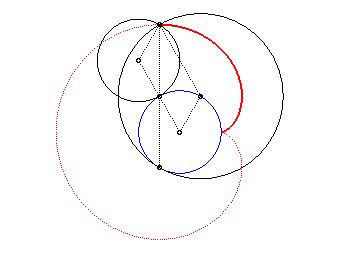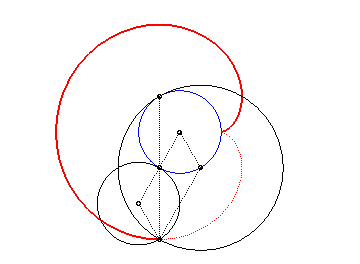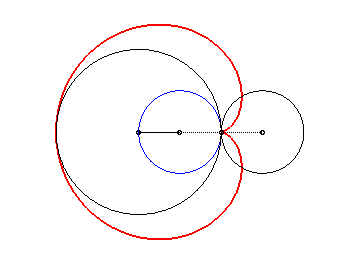
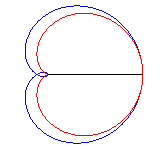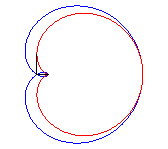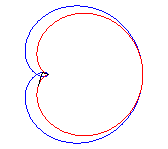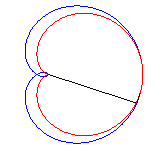
    3 b) la cardioïde est donc aussi l’enveloppe des cercles dont un diamètre joint un point fixe (ici O) d'un cercle (ici le cercle (C'), en rouge ci-dessous) à un autre point de ce cercle.

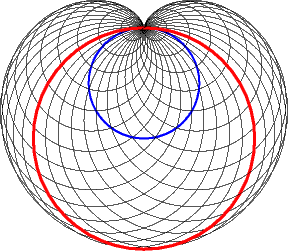
Le cercle bleu ci-dessus est le cercle des centres de la famille des cercles, c'est en fait la déférente de cette génération cyclique.

    3. c) une inverse de parabole par rapport à son foyer (ici, de la parabole d’équation , qui a O pour foyer) .

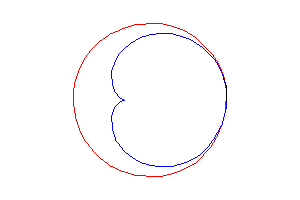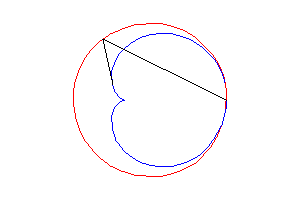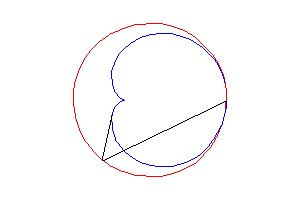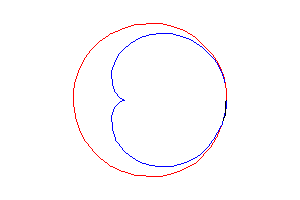
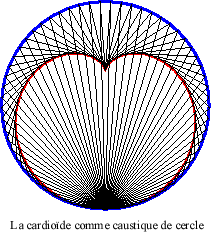
4) une caustique de cercle par réflexion avec source lumineuse sur le cercle (ici le cercle de centre (3a/2, 0) passant par O).
 

C'est cette propriété qui fait apparaître une cardioïde dans ce récipient conique rempli de lait (voir à surface caustique) :

5) une orthocaustique de limaçon trisecteur de pôle le sommet de la boucle.

6) une orthocaustique de sextique de Cayley de pôle le sommet de la boucle.

7) une podaire de cissoïde droite de pôle le point (4a , 0).

8) un cas particulier de spirale sinusoïdale.

9) une glissette : la cardioïde est le lieu du sommet d'une parabole variable de foyer fixé et passant par un point fixé :

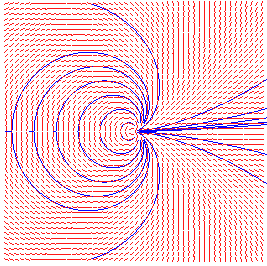
10) Les lignes de champ du champ complexe défini par  sont des cardioïdes.

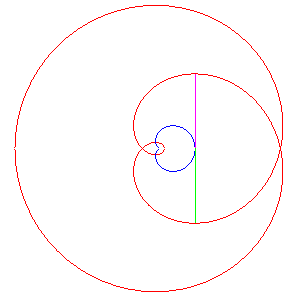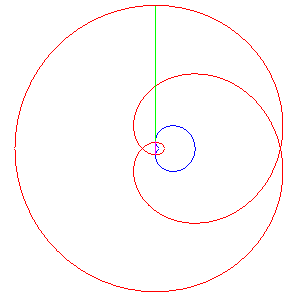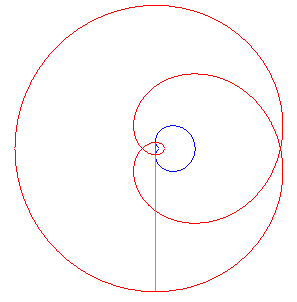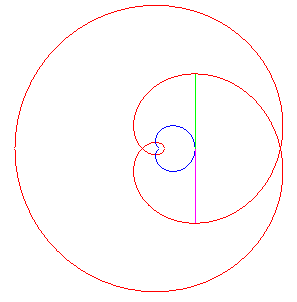
Comme pour toute courbe cycloïdale, la développéede la cardioïde est une cardioïde semblable, image par l’homothétie de centre W , de rapport –1/3.
L'une des développantes est donc une cardioïde ; les autres sont auto-parallèles (animation de la construction de l'une d'entre elles ci-contre).
La courbe parallèle à la distance d a pour paramétrisation  ; grâce au point de rebroussement, elle est elle-même parallèle à la distance –d, donc auto-parallèle. Les points de rebroussement décrivent bien la développée.
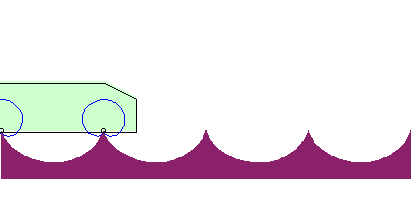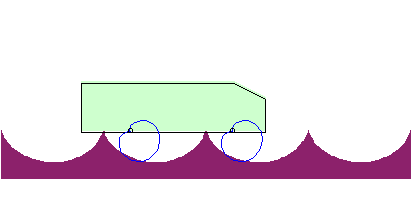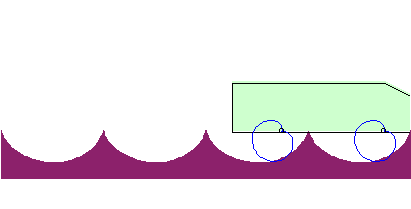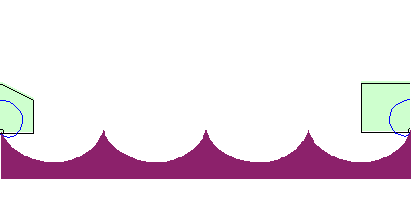
La roulette de la pointe de la cardioïde roulant sur une cycloïde de même longueur est rectiligne :

L'orthoptique de la cardioïde est formée d'un cercle et d'un limaçon de Pascal.

Voir une conchoïde de cardioïde en forme de coeur, comme dans les cartes.

On retrouve aussi la cardioïde dans certaines cycloïdes sphériques et dans les multicardioïdes.

On trouve enfin une belle cardioïde au centre de l’ensemble de Mandelbrot :

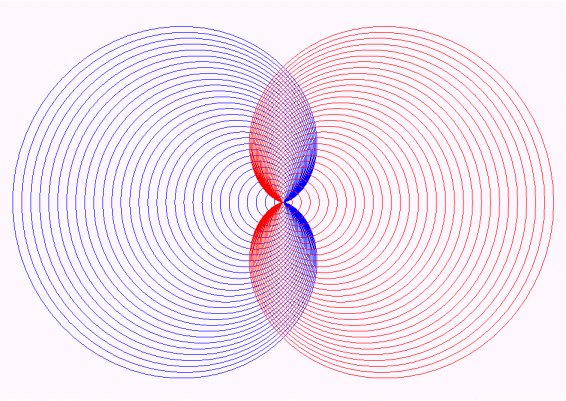Les cardioïdes r = a (1 + cos q ) pour a > 0 et leurs symétriques par rapport à Oy forment un réseau orthogonal.

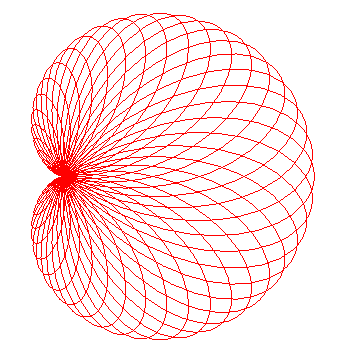Les courbes d'équation  (cissoïdales de cercle passant par O et rosace de même rayon) offrent un élégant remplissage de la cardioïde  (idée de Thierry LEGAY) . Ici, k = 55/17.

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2020