et 
:
.| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
COURBE CISSOÏDALE
Cissoid
curve, kissoidale kurve
| Du grec Kissos : lierre. |
| Équation polaire de la cissoïdale de pôle
O
des
courbes
et
:
. |
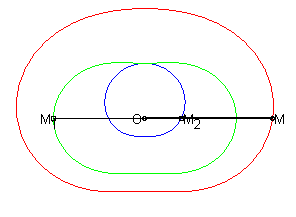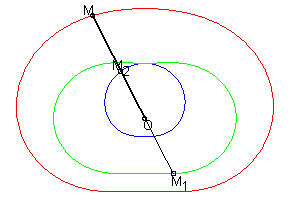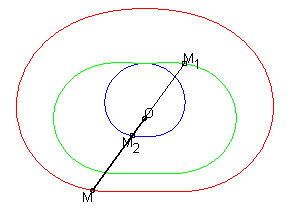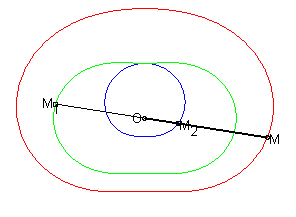
La (courbe) cissoïdale de deux courbes 
et 
relativement
à un point O est le lieu 
des points M tels que 
où M1 est un point de
et M2
un point de ,
M1
et M2 étant alignés
avec O.
La cissoïdale est donc la courbe
médiane de pôle O des courbes 
et 
images
de et
par une homothétie de centre O et de rapport 1/2.
On définit parfois la cissoïdale comme le
lieu des points M tels que 
; cela revient bien sûr à changer
en sa symétrique par rapport à O, par rapport à
la définition que nous avons prise.
et sont
deux droites parallèles, la cissoïdale est une troisième
droite parallèle.
et sont
deux droites sécantes, les cissoïdales sont des hyperboles
passant par O, d’asymptotes
et .
est un cercle et que O est le centre de ce cercle, on obtient les
conchoïdes
de la courbe .
est une conique,
une droite, O sur la conique, on obtient les cissoïdales
de Zahradnik.
et sont
des cercles et O est sur l'un des cercles, on obtient les quartiques
bicirculaires rationnelles.
et sont
des cercles et que O est le milieu des centres, on obtient les courbes
de Booth, dont la lemniscate
de Bernoulli est un cas particulier.
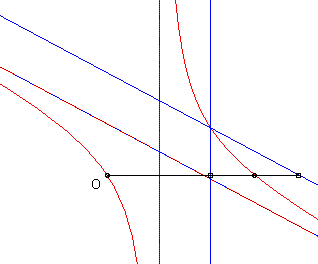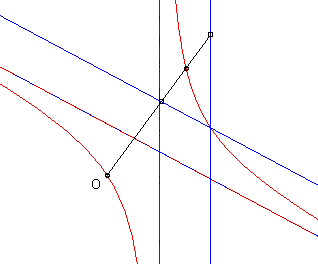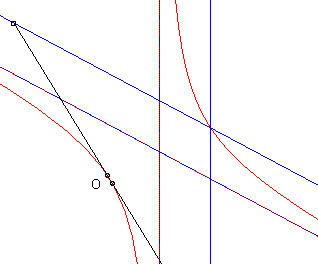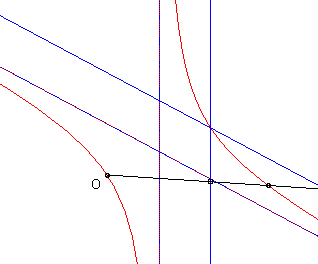
- Le folium parabolique est la cissoïdale d'une droite et d'une parabole semi-cubique.
- les scarabées sont les cissoïdales de cercle et trèfle à 4 feuilles.
Remarque : lorsque les deux courbes
et sont
confondues, la cissoïdale comprend l'homothétique de cette
courbe de centre O et de rapport deux, mais aussi éventuellement
une autre partie (car les points M1
et M2 peuvent être distincts).
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL, Jacques MANDONNET 2005