Équation polaire : . Équation cartésienne : . Cas  suivant que .

Les quartiques bicirculaires rationnelles sont les quartiques bicirculaires possédant un point singulier réel - ici, O - qui est forcément unique (les points cycliques sont les deux autres points singuliers) ; la quartique est dite crunodale, cuspidale ou acnodale suivant que ce point singulier est un point double à tangentes distinctes, un point de rebroussement ou un point isolé.

Comme les cubiques circulaires rationnelles, elles possèdent la propriété d’avoir 4 définitions géométriques remarquables équivalentes.

1) Ce sont les podaires de coniques à centre (ici podaire par rapport à O de la conique  ).
Elles sont crunodales, cuspidales, ou acnodales suivant que le point O est extérieur à la conique, sur la conique ou intérieur à la conique.
 

cas crunodal

cas cuspidal

cas acnodal

Exemples : lorsque la conique est un cercle, on obtient les limaçons de Pascal (dont la cardioïde) et lorsque O est le centre de la conique, on obtient les courbes de Booth (dont la lemniscate de Bernoulli).

Cette définition comme podaire entraine une définition comme roulette d'une conique à centre roulant sur une conique égale, et aussi comme courbe de l'antiparallélogramme articulé.

Trace d'un point d'une ellipse roulant sur une ellipse égale : on obtient une pseudo-cardioïde.

2) Ce sont donc les enveloppes de cercle de diamètre d'extrémités un point fixe (ici, O) et un point décrivant une conique à centre.
 

cas crunodal

cas cuspidal

cas acnodal

3) Ce sont les inverses de coniques par rapport à un point non situé sur la conique (ici, de la conique d'équation :  où p est la puissance d'inversion). Lorsque le centre d'inversion est sur la conique, on obtient une cubique circulaire rationnelle.
La quartique est crunodale, cuspidale, ou acnodale suivant que cette conique est une hyperbole, une parabole ou une ellipse.
 

cas crunodal

cas cuspidal

cas acnodal

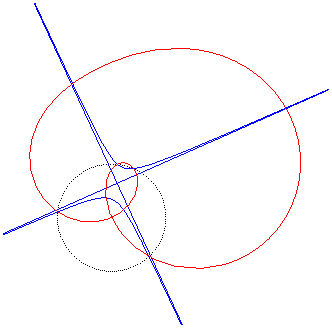
Animation de l'inverse d'une hyperbole équilatère ; le centre d'inversion décrit le cercle pointillé. Les deux branches de l'hyperbole deviennent deux boucles qui se rejoignent en un point double. La quartique bicirculaire a une forme de huit tordu lorsque le centre d'inversion est entre les deux branches de l'hyperbole ; sinon les deux boucles sont incluses l'une dans l'autre.

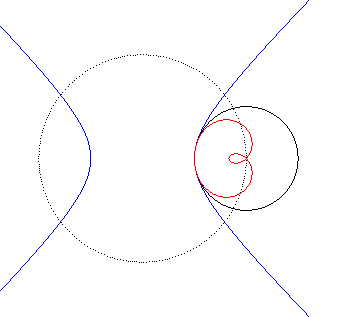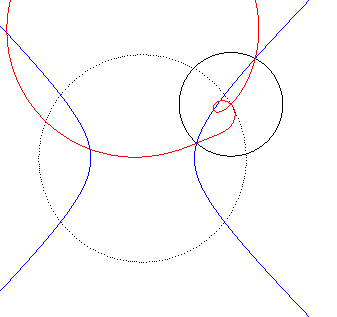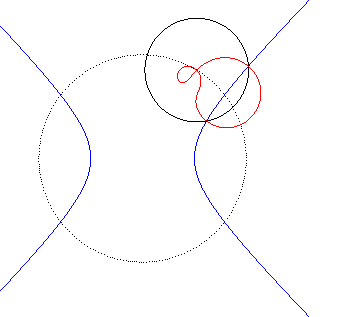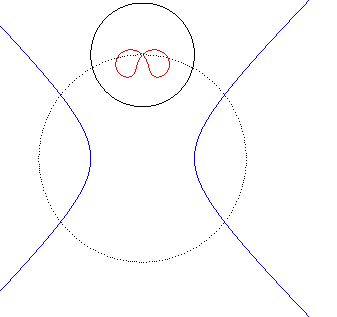4) Ce sont les cissoïdales de deux cercles par rapport à l'un des point de l'un des cercles, le premier cercle de centre  passant par O et le deuxième de centre  et de rayon a. La quartique est crunodale, cuspidale, ou acnodale suivant que ces cercles se coupent, sont tangents ou disjoints.
 

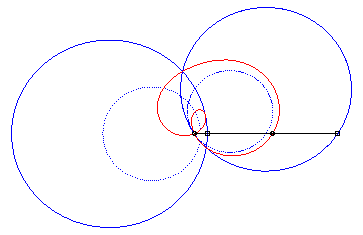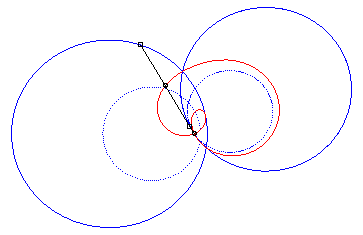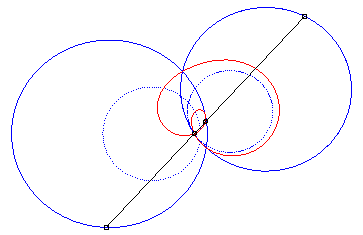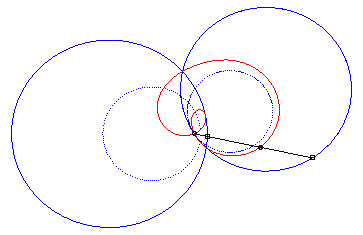
cas crunodal

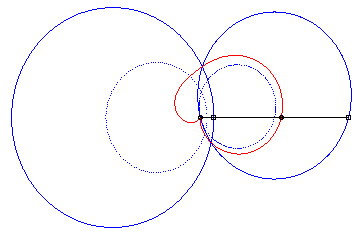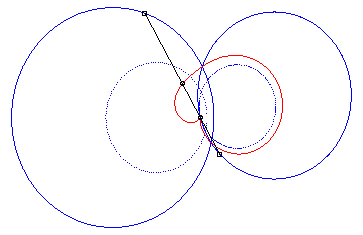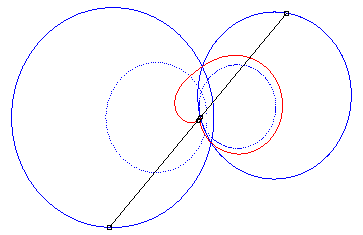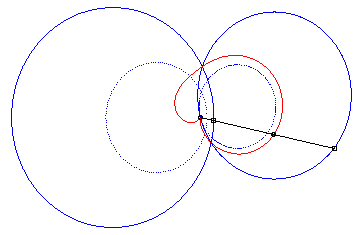
cas cuspidal

cas acnodal

Voir aussi comme cas particulier la conchoïde de Dürer.
 
 

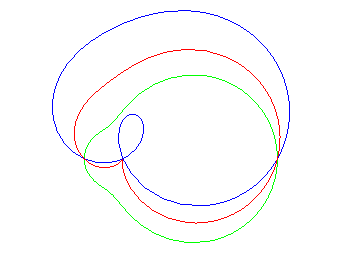
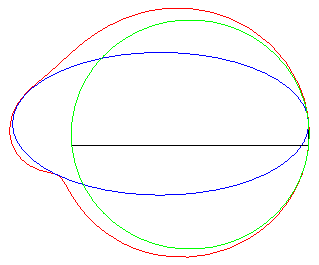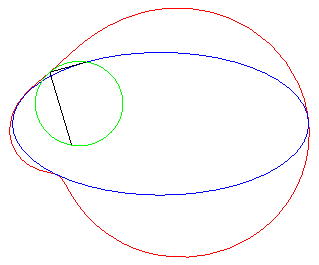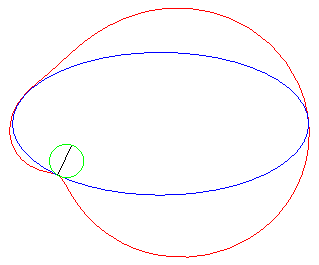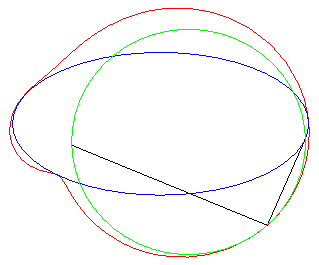
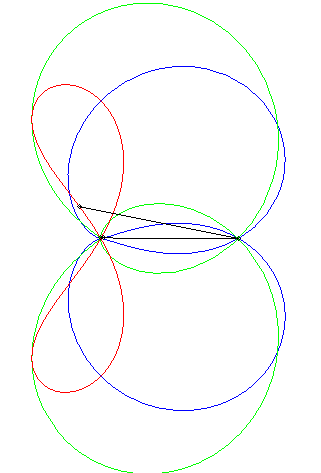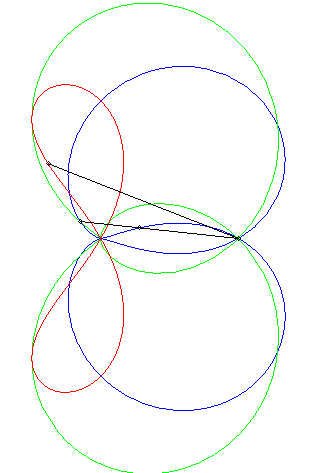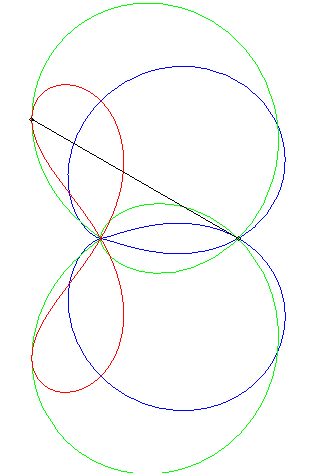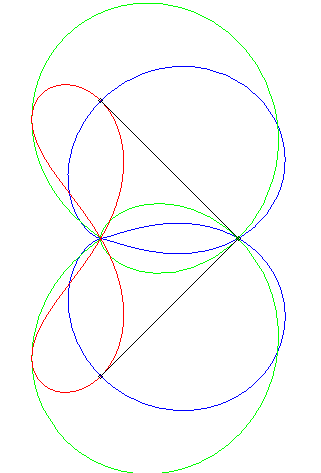
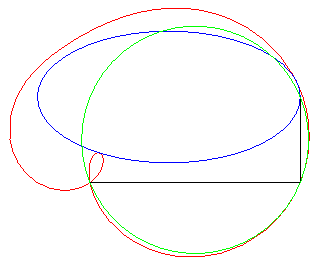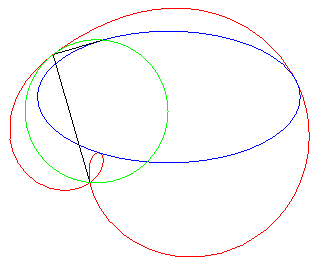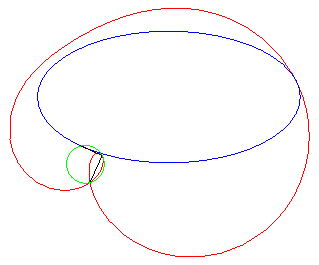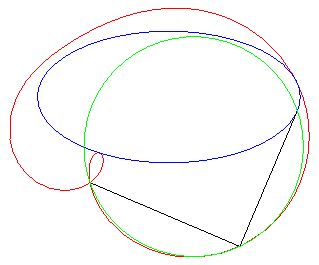
Un exercice sur les complexes qui aboutit à une quartique bicirculaire rationnelle : "Déterminer le lieux des points d'affixe z tels que (1, z3, z4) sont alignés" (voir ici). On obtient l'axe des x plus la quartique d'équation (x2 + y2  + x)2 = y2 – 2x2, , quartique qui est l'inverse par rapport à O de l'hyperbole  3x2  – y2 + 2x + 1 = 0 (cette dernière étant le lieu d'alignement de (1, z, z4) ) ; c'est donc une quartique crunodale. Ci-contre en rouge, le lieu de z, en bleu celui de z3, en vert celui de z4. Un trait noir relie z, 1, z3, et z4 ; constater que (1, z3, z4) sont alignés.

Autre exercice aboutissant à une quartique bicirculaire rationnelle (voir ici). Le point I étant le milieu d'un segment [AB], déterminer le lieu des points M d'où l'on voit le segment [AI] d'un angle double de celui du segment [IB] (ou, ce qui est équivalent, tel que la médiane (MI) du triangle MAB en soit aussi une trisectrice). En prenant A(–1,0), B(1,0), M(x,y), on obtient l'axe des x plus la quartique d'équation (x2 + y2  + x)2 = 4x2 – y2, quartique qui est l'inverse par rapport à O=I  de l'hyperbole  3x2 – y2 – 2x – 1 = 0 : c'est donc une quartique crunodale. Paramétrisation : ; pour t entre  et , on a , donc l'angle en M du triangle AMB varie entre  et 0.

 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2020