QUARTIQUE DE PLÜCKER, COURBE DE L'ESPERLUETTE
Plucker's
quartic, ampersand curve, Plückersche Quartik,
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
QUARTIQUE DE PLÜCKER, COURBE DE L'ESPERLUETTE
Plucker's
quartic, ampersand curve, Plückersche Quartik,
| Courbe étudiée par Plücker en 1839.
Julius Plücker (1801-1868) : mathématicien et physicien allemand. L'apellation "ampersand curve" a été donnée par [Cundy et Rolett]. Sites : perso.univ-rennes1.fr/christophe.ritzenthaler/cours/elliptic-curve-course.pdf (p. 43) library.msri.org/books/Book35/files/gray.pdf (p 122) |
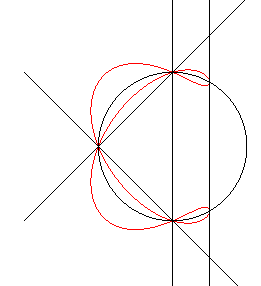
| En 1839, J. Plücker a construit une quartique
ayant ses 28 bitangentes réelles et distinctes.
Équation :  .
La figure de droite montre les 4 droites |
 |
|
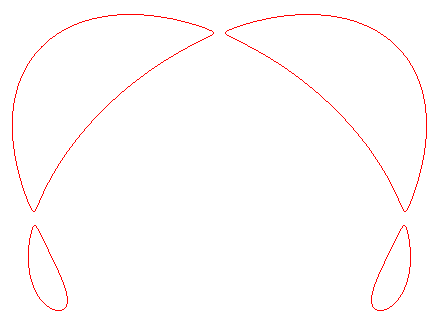
Pour une cte >0 assez petite, la quartique est formée de quatre composantes, ayant chacune une partie concave, appelées "ménisques", donc ayant chacune une bitangente ; ajoutées aux 6 fois 4=24 bitangentes reliant deux composantes, cela fait bien 28 en tout. |
 |
Voir la quartique de
Salmon pour une courbe plus simple à 28 bitangentes.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2014
,
et le cercle 
ayant servi à la détermination de cette courbe, et la courbe
dans le cas où la constante est nulle (quartique rationnelle à
3 points doubles). C'est cette courbe que Cundy et Rolett désignent
par "ampersand curve".