Quartique de Salmon

Salmon quartic, Salmonsche Quartik

Courbe étudiée par Salmon en 1852 (voir higher plane curves p. 45)
George Salmon (1819-1904) : mathématicien anglais.

Équation cartésienne : , a, b > 0 , ou .
Paramétrisation cartésienne : .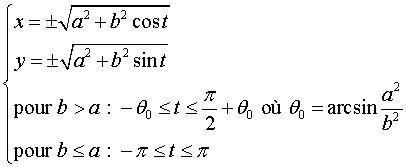
Quartique de genre 3 pour b différent de a et de , décomposée pour b = a, de genre 2 pour b = .

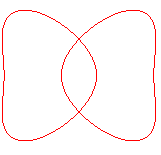
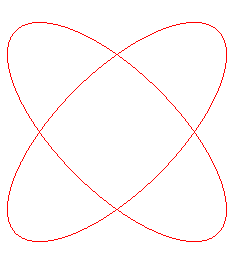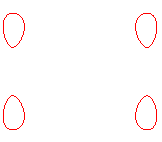
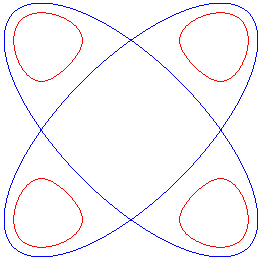
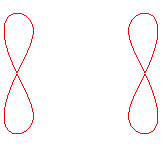
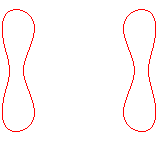
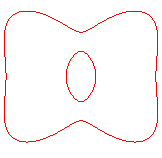
Pour b = a , la quartique se décompose en deux ellipses (cf la deuxième équation) Pour b < a, elle est formée de 4 composantes connexes entourant les sommets d’un carré (de coordonnées ), ce qui est le maximum possible pour une quartique.

Pour a < b < , elle est formée de 2 composantes connexes, la composante centrale dégénérant en un point isolé pour b = .
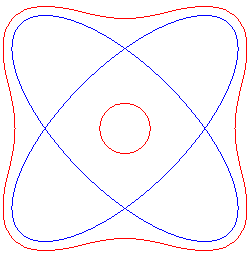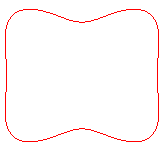
La quartique est dite "annulaire". Pour b > , il n'y a plus qu'une composante.

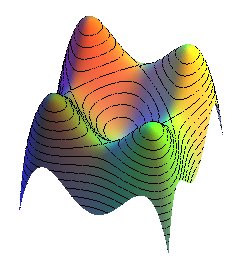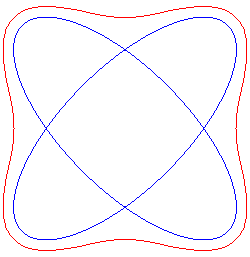
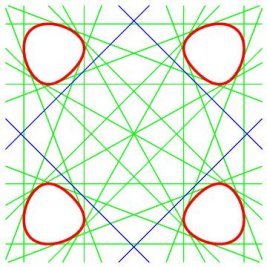
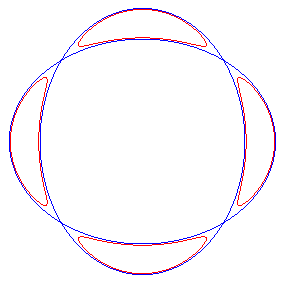
Tout ceci se voyant bien sur la surface dont les quartiques de Salmon sont les courbes de niveau. Pour 0 < b < a, la quartique de Salmon possède visuellement 4 fois 6 = 24 bitangentes, comme auraient 4 cercles dans un plan. Quartique de Salmon et 6 de ses 24 bitangentes

Pour , les 4 composantes ont une partie concave et possèdent donc chacune une bitangente.
La quartique de Salmon possède donc dans ce cas 24+4=28 bitangentes réelles, maximum possible pour une quartique.

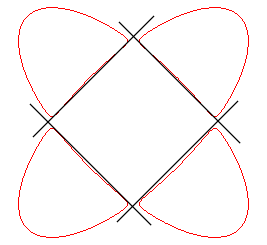Les 4 bitangentes supplémentaires dans ce cas.
Or une quartique ne peut avoir que 28, 16, ou au plus 8 bitangentes réelles.
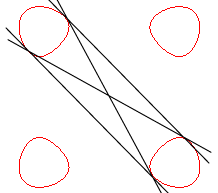
Où sont les 4 bitangentes manquantes dans le cas où les 4 composantes sont convexes ?
Elles sont bien réelles (en bleu ci-contre), mais leurs points de tangence avec la quartique sont à coordonnées complexes !

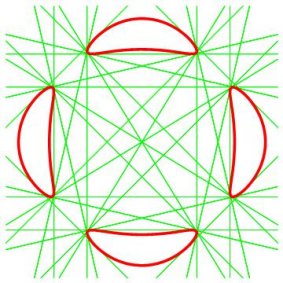
Pour obtenir le même phénomène des 4 composantes et des 28 bitangentes, on peut croiser des ellipses quelconques de sorte à accentuer la concavité des "ménisques".
Ci-contre, la courbe
pour b=0,3a et k=0,01, avec ses deux ellipses directrices, et ses 28 bitangentes.
(Cf. la courbe de Trott).

Cf. aussi la quartique de Plücker, qui est l'exemple historique de quartique à 28 bitangentes.

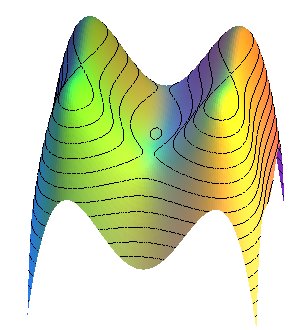
Salmon a plus généralement étudié la quartique
dont les différentes formes indiquées ci-dessous se voient bien sur la figure de la surface ci-contre.

b < a1 < a2 b=a1<a2 a1 < b < a2 a1 < a2 = b a1<a2<b<(a1^4+a2^4)^(1/4) a1<a2<(a1^4+a2^4)^(1/4)<=b

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres

Pour b = a , la quartique se décompose en deux ellipses (cf la deuxième équation)		Pour b < a, elle est formée de 4 composantes connexes entourant les sommets d’un carré (de coordonnées ), ce qui est le maximum possible pour une quartique.
Pour a < b < , elle est formée de 2 composantes connexes, la composante centrale dégénérant en un point isolé pour b = . La quartique est dite "annulaire".		Pour b > , il n'y a plus qu'une composante.
Tout ceci se voyant bien sur la surface dont les quartiques de Salmon sont les courbes de niveau.		Pour 0 < b < a, la quartique de Salmon possède visuellement 4 fois 6 = 24 bitangentes, comme auraient 4 cercles dans un plan.	Quartique de Salmon et 6 de ses 24 bitangentes
Pour , les 4 composantes ont une partie concave et possèdent donc chacune une bitangente. La quartique de Salmon possède donc dans ce cas 24+4=28 bitangentes réelles, maximum possible pour une quartique.	Les 4 bitangentes supplémentaires dans ce cas.	Or une quartique ne peut avoir que 28, 16, ou au plus 8 bitangentes réelles. Où sont les 4 bitangentes manquantes dans le cas où les 4 composantes sont convexes ? Elles sont bien réelles (en bleu ci-contre), mais leurs points de tangence avec la quartique sont à coordonnées complexes !

b < a1 < a2	b=a1<a2	a1 < b < a2	a1 < a2 = b	a1<a2<b<(a1^4+a2^4)^(1/4)	a1<a2<(a1^4+a2^4)^(1/4)<=b