Du grec huperbolê "dépassement, excès" de huper "au-dessus, au delà" et de ballein "lancer". Nom donné par Apollonius de Perge. Voir sur cette page d'Alain Esculier les programmes de tracé des animations.

 

Équation cartésienne réduite : . a = demi axe focal (ou transverse), b = demi axe non focal (ou non transverse). = demi-distance focale. = excentricité, p =  = paramètre. F(c, 0) et F'(– c, 0) : foyers de l’hyperbole. (D), (D'), droites d'équation x = a2/c et x = – a2/c  : directrices de l’hyperbole. K : pied de la directrice sur l'axe Ox. d = FK  = b2/c . L'hyperbole est dite équilatère lorsque a = b, soit  , c’est-à-dire lorsque les asymptotes sont perpendiculaires. L'hyperbole d'excentricité 2 est une trisectrice.

Équation cartésienne rapportée aux asymptotes : XY =  , le repère étant orthogonal ssi l'hyperbole est équilatère. Paramétrisation cartésienne 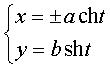:  (avec  ; forme choisie pour la formule d'abscisse curviligne et les suivantes). ou  (avec). Équation polaire : . Abscisse curviligne : . Rayon de courbure : . Équation bifocale : . Équation polaire (pôle F, axe Fx) : . Équations cartésienne et polaire dans un repère d’origine un sommet et d’axe des abscisses l’axe focal : , .

Les hyperboles sont les coniques d'excentricité  > 1.

Elles ont été historiquement définies comme section de cône de révolution par un plan faisant avec l’axe du cône un angle inférieur à celui de l’angle entre une génératrice et l’axe.
 

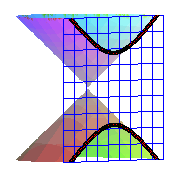
hyperbole = intersection non connexe d'un cône et d'un plan

Application : la trace d'un cône de lumière sur un mur a un contour hyperbolique, si elle est non bornée.

Mais plus généralement toute section d’une quadrique par un plan, ayant deux composantes connexes, est une hyperbole.

L'hyperbole possède de nombreuses définition géométriques planes :

1) Définition bifocale.
     - L'hyperbole est le lieu d'un point dont la différence des distances à deux points fixes F et F' est constante en valeur absolue (voir l’équation bifocale) ; d'où les constructions mécaniques suivantes :
 

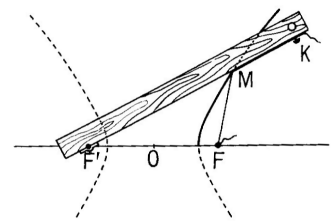
Méthode d'Ibn Sahl. Figure tirée de la bible : le Lebossé Hémery

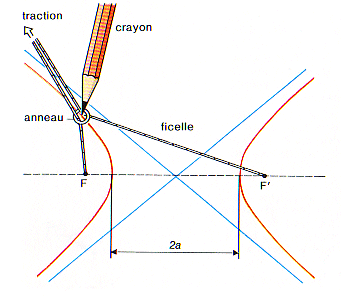
Les deux fils ne doivent ici pas coulisser entre eux (méthode de Képler).

 

Tracé par mécanisme à trois barres, les deux manivelles ayant pour longueur 2a, et la bielle 2c ; les prolongements des 2 bielles se coupent en un point M décrivant l'hyperbole car  MF' – MF = MF' – MG' =F'G'= 2a.

Cette propriété a été appliquée dans le système d'aide à la navigation appelé LORAN.

La construction des foyer et directrice de l'hyperbole définie comme section d'un cône est donnée par le théorème de Dandelin illustré ci-dessous :
 

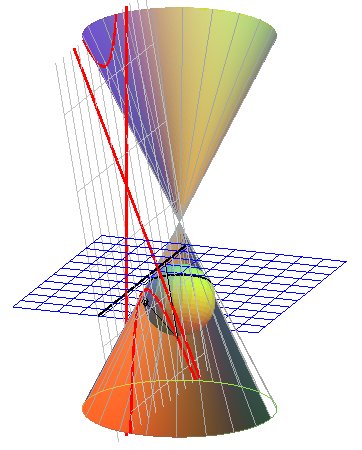Les 2 sphères inscrites dans le cône et tangentes au plan de l'hyperbole le sont aux foyers de celle-ci, et les plans des cercles de contact coupent le plan de l'hyperbole en les 2 directrices.

1 bis) L'hyperbole est le lieu d'un point M tel que la tangente en M à ce lieu est la bissectrice intérieure de l'angle F'MF :

Les angles indiqués sont toujours égaux

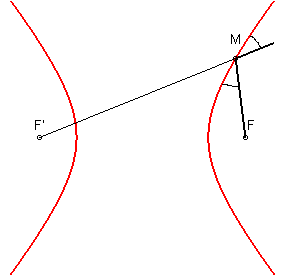
Applications :

Principe du télescope de Cassegrain

Si l'on vise le foyer de cette branche d'hyperbole, la balle ira dans le trou en un rebond.

 

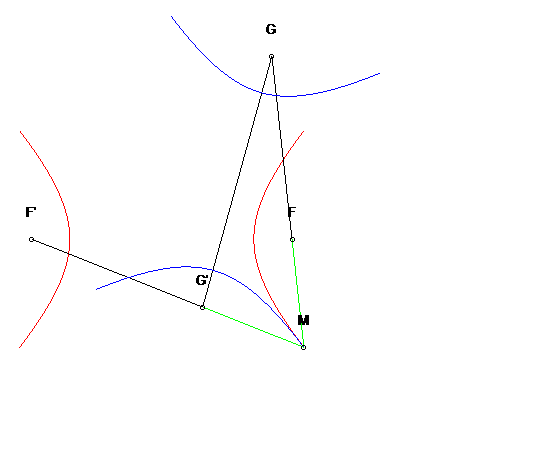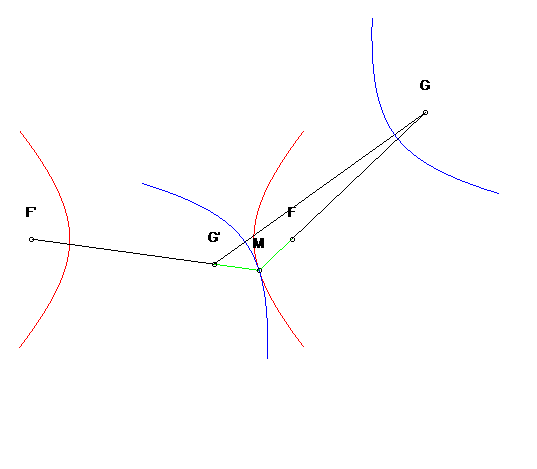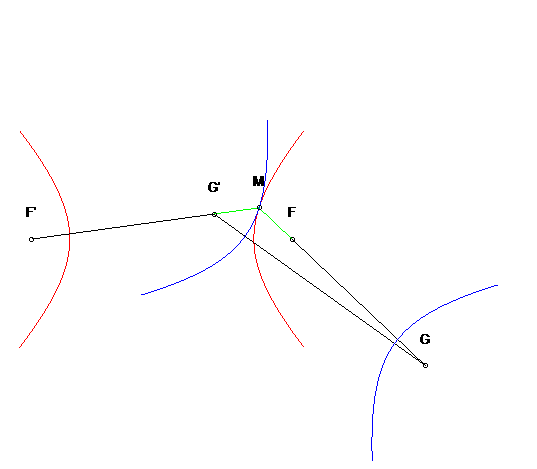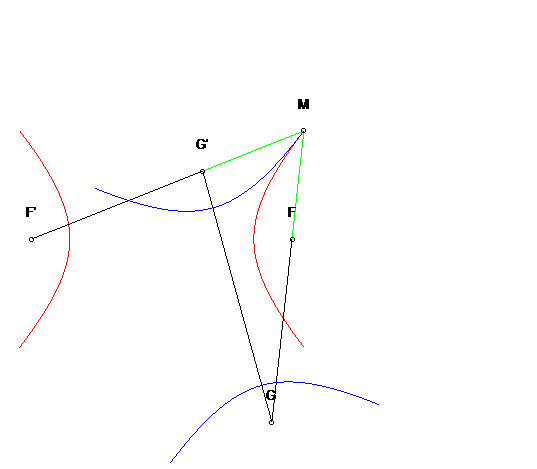
Autre application : en tout point M de l'hyperbole de départ, l'hyperbole symétrique par rapport à la tangente en M est l'hyperbole de foyers les points G et G' vus ci-dessus lors de la construction par trois-barres. De plus, cette hyperbole roule sans glisser sur la première.
Si l'on se place dans le plan lié à F et G, les deux hyperboles tournent autour de F et G en restant constamment tangentes, avec un roulement sans glissement : c'est la propriété d'isotrépence de l'hyperbole par rapport à un foyer.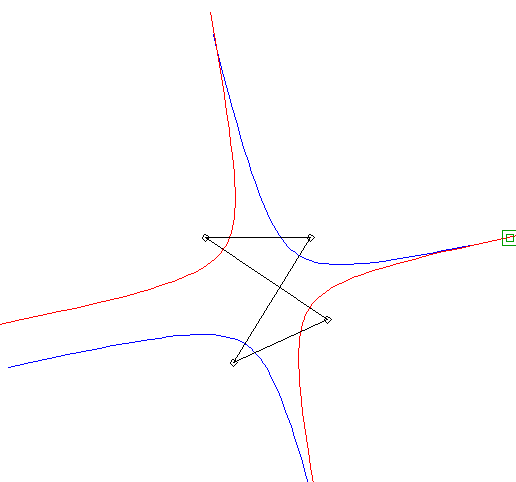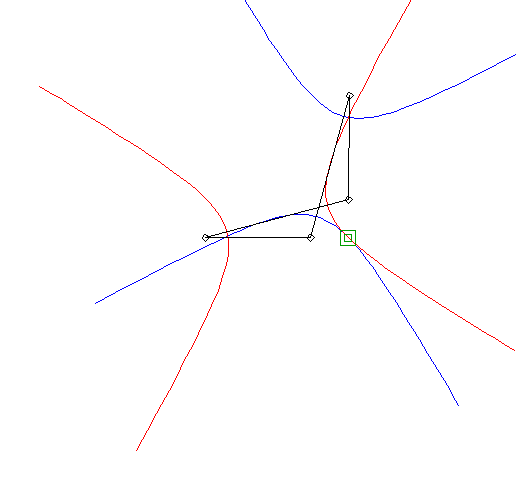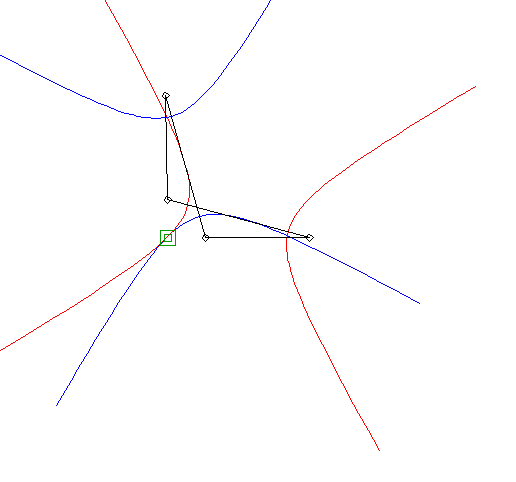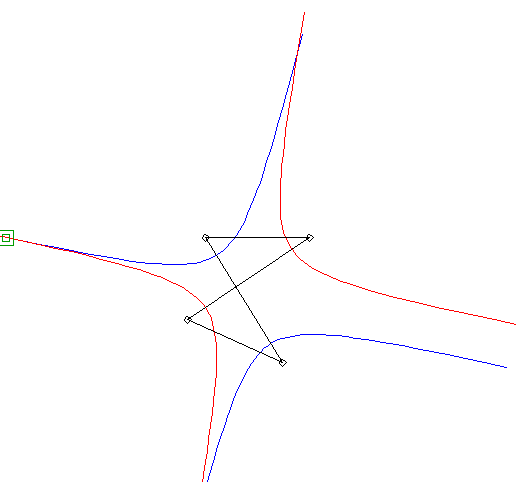

2) Définition par courbe d'équidistance entre un point et un cercle, autrement dit comme isotèle de cercle.
L'hyperbole est le lieu des points équidistants d'un cercle (appelé cercle directeur, de centre l'un des foyers F' et de rayon 2a) et d'un point situé à l'extérieur de ce cercle (qui est l'autre foyer F) ; autrement dit, c'est le lieu du centre d’un cercle variable astreint à passer par F et à être tangent à C(F', 2a).
 

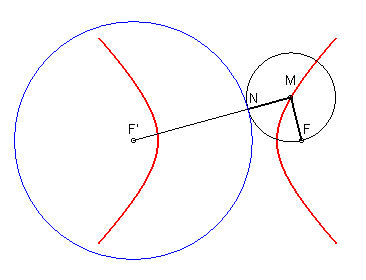
première branche MF = MN (= MF' - 2a ) :  l'hyperbole est la courbe d'équidistance du foyer F et du cercle directeur bleu.

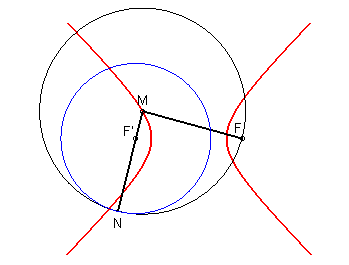
deuxième branche MF = MN (= 2a - MF'  )

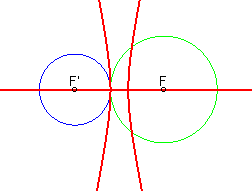
Plus généralement les courbes d'équidistance entre deux cercles extérieurs sont des réunions d'hyperboles :
 

	Les points rouges sont les points "équidistants" du cercle bleu et du cercle vert
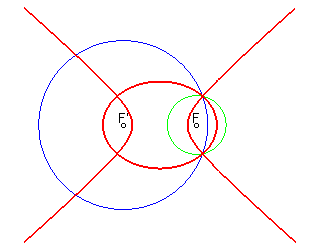
		Lorsque les cercles sont séquents, la courbe d'équidistance est réunion d'une ellipse et d'une d'hyperbole.

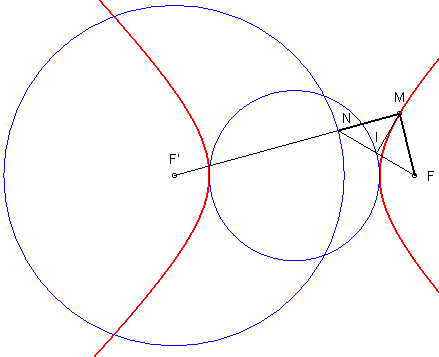
3) Définition tangentielle par antipodaire de cercle.
L'hyperbole est l’enveloppe de la perpendiculaire en I à la droite (FI), I décrivant le cercle principal C(O, a) (autrement dit, l’antipodaire de ce cercle par rapport à F), ou encore l’enveloppe de la médiatrice du segment [FN], N décrivant le cercle directeur C(F', 2a) (qui est l’orthotomique de l’hyperbole par rapport à F').

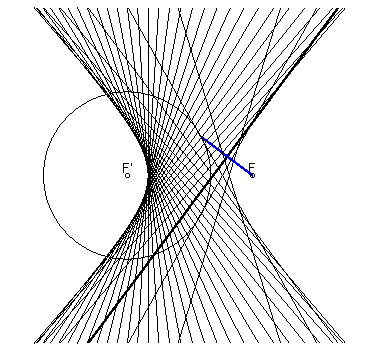
Application : si vous tracez un cercle sur une feuille de papier, marquez un point F à l'extérieur, et formez un certain nombre de pliures en amenant le point F sur un point du cercle, les pliures seront enveloppées par une hyperbole.

Ceci permet aussi l'élégante construction par système articulé ci dessous :

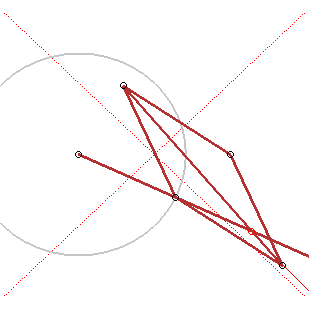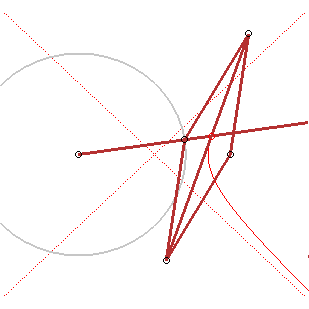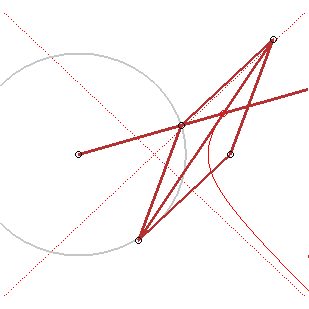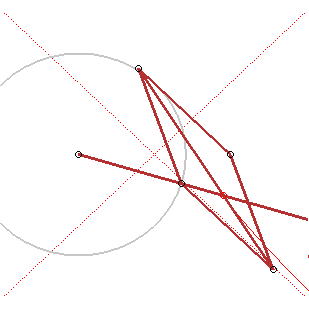
4) Définition par foyer et directrice.
L'hyperbole est le lieu d’un point M tels que où H est le projeté de M sur la directrice (D).

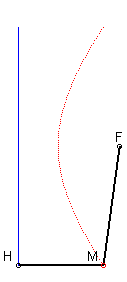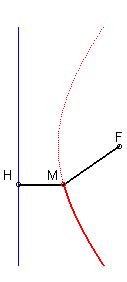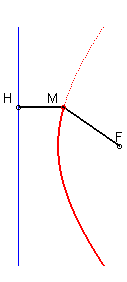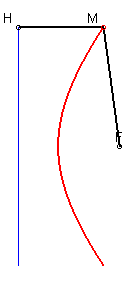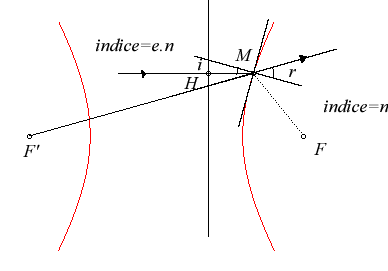
     Les longueurs MH et MF ont un rapport constant (ceci vaut aussi pour l'autre branche)

Interprétant la quantité MF - eMH'  comme un chemin optique, cela signifie que si l'extérieur de l'hyperbole est constitué d'un milieu d'indice de réfraction n et l'intérieur d'indice e.n, les rayons incidents parallèles à l'axe de l'ellipse situés du côté de (D') seront réfractés en des rayons tous issus de F. En d'autres termes, la caustique par réfraction de l'hyperbole pour des rayons parallèles à l'axe est réduite aux deux foyers.

MF'- eMH= 2a, d'où

Ceci a comme application la conception de lentilles divergentes (l'indice de réfraction de la lentille doit être égal à e) :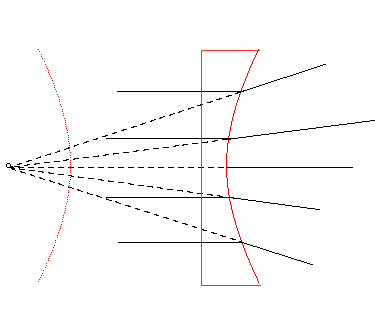

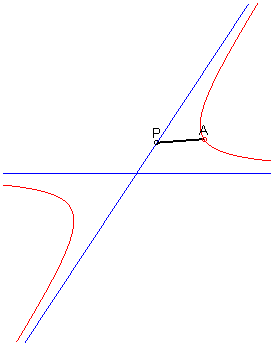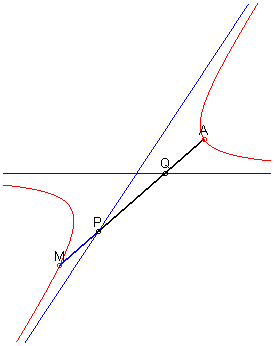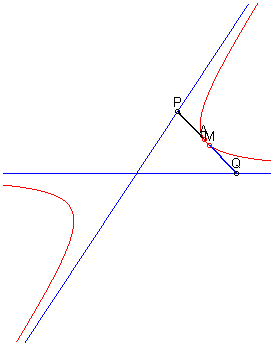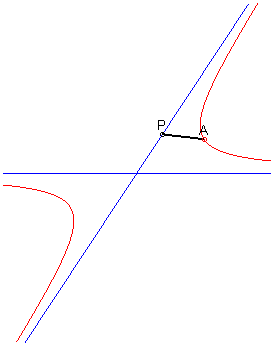
5) Définition comme cissoïdale de deux droites sécantes :
   Étant donné deux droites sécantes et un point A en dehors de ces droites, le lieu des points M tels que  où P et Q sont les deux points d'intersection avec les asymptotes d'une droite variable passant par A, est l'hyperbole passant par A et d'asymptotes les deux droites de départ  (on en déduit facilement que l’hyperbole est la cissoïdale de deux droites sécantes).

C'est cette propriété qui est à la base des trace-hyperbole suivants :
 

Trace-hyperbole de Descartes

Trace-hyperbole de L'Hospital

Voici encore deux mécanismes pour tracer les hyperboles :
 

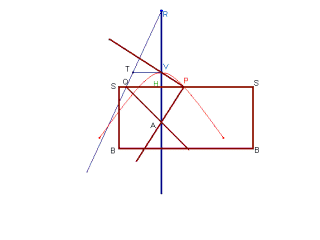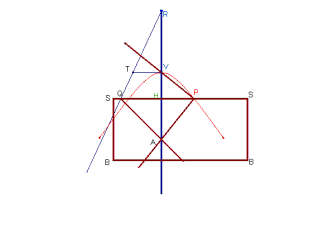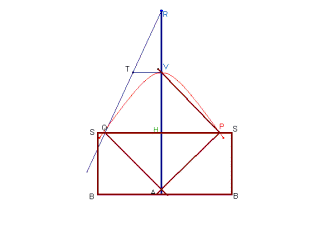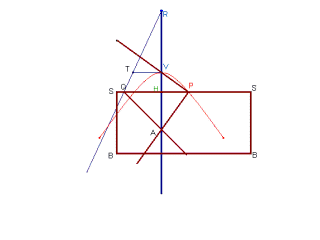
Trace-hyperbole de Cavalieri

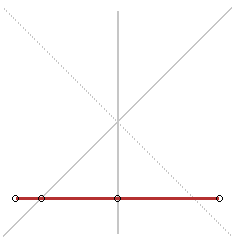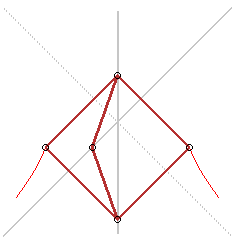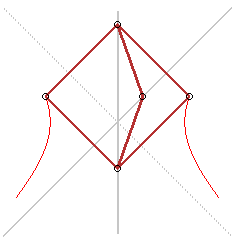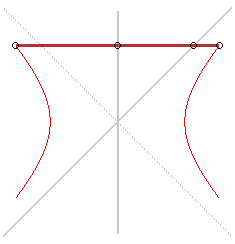
Trace- hyperbole de Delaunay

6) Définition comme lieu des points dont les produits des distances à deux droites est constant.
 

On donne deux droites sécantes D et D' faisant entre elles un angle de  ; le lieu des points dont le produit des distances à D et D' est constant égal à C²  est la réunion des deux hyperboles ayant pour asymptotes D et D' et dont la demi-distance focale est .

courbes de niveau du produit des distances aux deux droites bleues

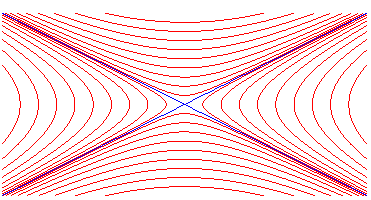Voici aussi une autre génération tangentielle :
 

Les droites joignant deux points ayant des mouvements circulaires uniformes de même période sont enveloppées par une hyperbole ; ceci vaut donc pour des tableaux de fils à deux bords circulaires et mêmes nombres de clous sur chaque bord.

Voir encore sur la page de l'hyperbole équilatère la construction comme enveloppe de triangle.

La développée de l'hyperbole est une demi-courbe de Lamé, d'équation .

Voir aussi la page spécifique à l'hyperbole équilatère, la trompette de Gabriel  et les hyperboloïdes.
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL, Jacques MANDONNET,  Alain ESCULIER 2012