Courbe étudiée par Maclaurin en 1742, Plateau en 1828 et Kempe en 1895. Colin Maclaurin (1698-1746) : mathématicien écossais. Autres noms : sectrice de Plateau, courbe isocyclotomique, araignée (Heymann 1899). Loria p. 460.

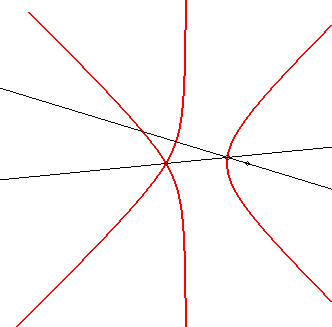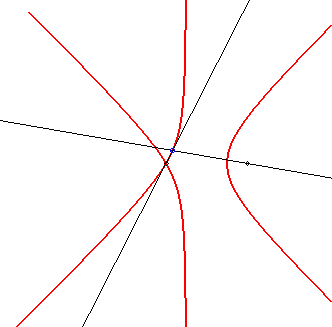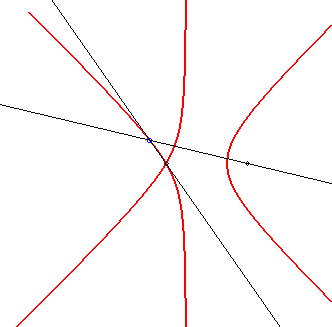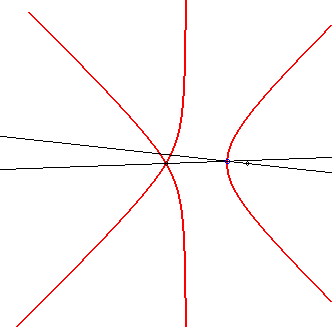
Les sectrices de Maclaurin sont les lieux des points d'intersection de deux droites pivotant uniformément chacune autour d'un point fixe.
 
 

Les points fixes étant O et A(a, 0), la vitesse angulaire de la droite DA passant par A étant k fois celle de la droite D0 passant par O, on obtient : Equation polaire dans le repère de pôle O : ,  étant l'angle  lorsque DO passe par A. Equation polaire dans le repère de pôle A : . On obtient toutes les sectrices en supposant |k| > 1 (échanger O et A revient à changer k en 1/k).

Les deux inverses d'une sectrice de Maclaurin par rapport aux 2 pôles sont encore des sectrices de Maclaurin : l'inverse de  par rapport à O est , et l'inverse de  par rapport à A est .

Lorsque  est constructible et lorsque k est entier, la sectrice de Maclaurin est une courbe |k|-sectrice, puisque le rapport entre les angles  est constamment égal à k. et c'est également une courbe |k–1|-sectrice car .

Cas particuliers remarquables pour  nul (c'est-à dire lorsque durant leur mouvement, les 2 droites viennent à être confondues):
 

k=	équation avec pôle O	équation avec pôle A	nom de la courbe	figure	remarque
2 (ou 1/2)			cercle		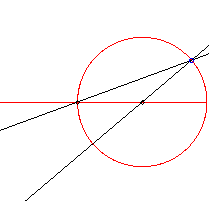Ceci équivaut au théorème de l'angle au centre. Quelle est la courbe décrite par le point d'intersection des deux droites passant par les aiguilles des secondes de deux montres placées dans un même plan ?
-1			droite		La bissectrice d'un triangle isocèle est aussi sa médiatrice !
3 (ou 1/3)			trisectrice de Maclaurin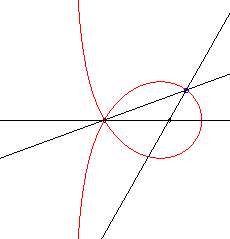
3/2 (ou 2/3)			limaçon trisecteur
–2 (ou –1/2)			hyperbole d'excentricité 2

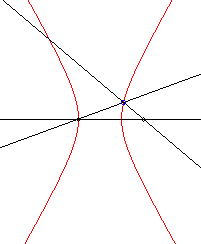Notons que parmi les 3 courbes , chacune est une inverse des deux autres (le cas k = 3 donnant les 3 courbes précédentes).

Cas particuliers avec  :

k = 1			cercle		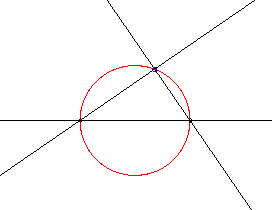Remarque : ceci équivaut au théorème de l'angle inscrit
k = 2			strophoïde droite
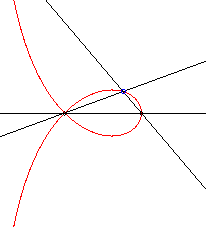k =  –1			hyperbole équilatère

Autre exemples :
 

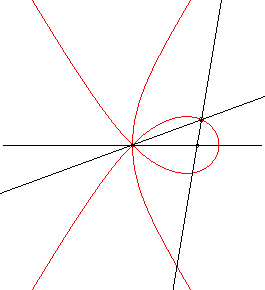
k = 4,  q0 = 0 ; c'est aussi une courbe trisectrice (cf. remarque ci-dessus).

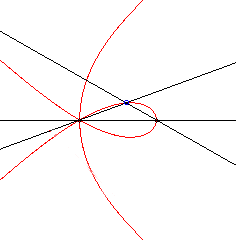
k = 3, q0 = p/2

Le cas limite où l'un des pôle est envoyé à l'infini n'est autre que celui de la quadratrice de Dinostrate et ses généralisations.
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2019