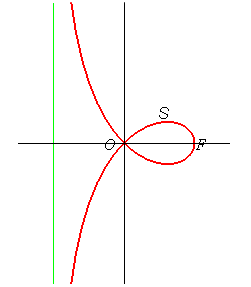
Coordonnées du point  S : ,  où  est le nombre d'or.

Équation polaire : (ou, tournée de  : ) Équation cartésienne : . Cubique circulaire rationnelle à point double. Paramétrisation cartésienne :  (avec ), ou  (avec ). Paramétrisation cartésienne rationnelle :    (avec ), soit en complexes : . Si l'on prend pour repère (F(0, a) (sommet de la boucle),  ), l’équation polaire se simplifie en :  (cas particulier de noeud) L'équation complexe se met alors sous la forme  avec  et une paramétrisation complexe est . Longueur de la boucle :. Aire de la boucle : . Aire entre la courbe et l'asymptote : .

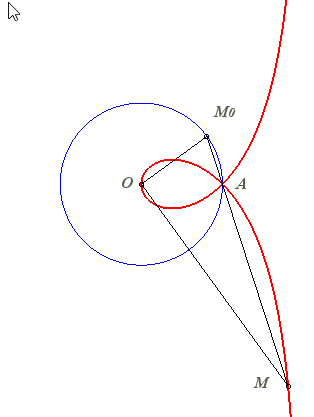
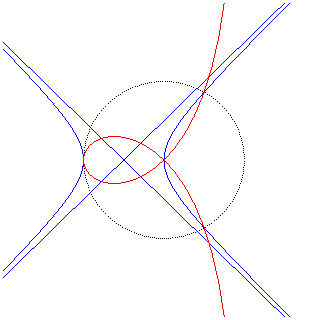
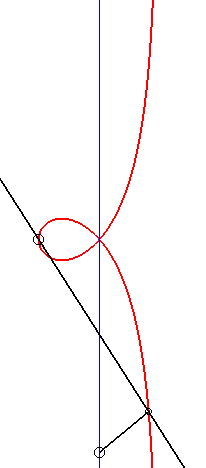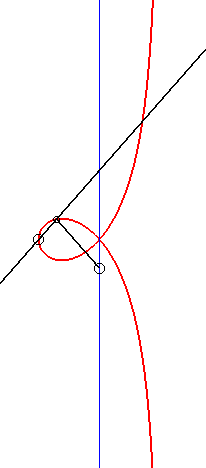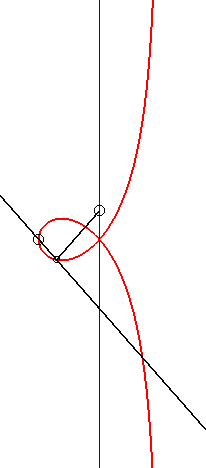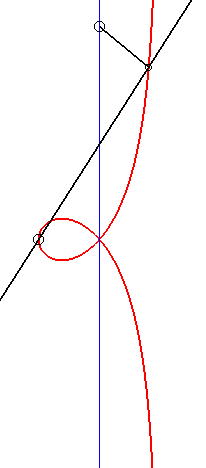
Deux points O et F étant donnés, la strophoïde droite de sommet (ou foyer) F et de centre O est le lieu des points M d'une droite variable (D) passant par F tels que PM = PO où P est le point d'intersection de la droite (D) avec la perpendiculaire (D₀) en O à (OF) (appelée axe de la strophoïde) ; autrement dit, c'est la courbe strophoïdale de (D₀) relativement à O et F (ici, O est l’origine du repère et F est le point (a, 0)) ; c'est un cas particulier de strophoïde générale. Le point F est appelé foyer car c'est le foyer singulier de cette cubique.

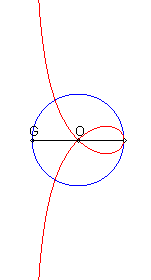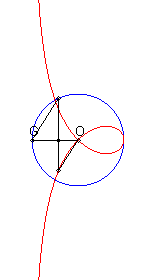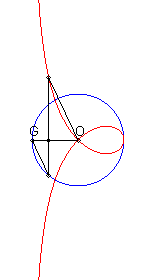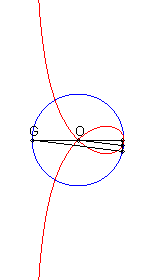
PM = PO

La strophoïde droite est donc aussi le lieu des points de contact des tangentes issues de F aux cercles (en bleu ci-contre) tangents en O à l'axe (D0), ou encore le lieu des intersections des cercles orthogonaux aux précédents (en vert ci-contre) tangents en O à (OF) avec les droites joignant F à leurs centres.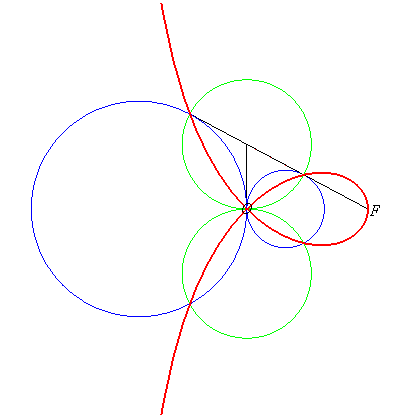

Voici trois autres constructions simples :
 

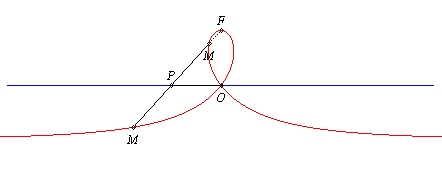
La strophoïde droite est le lieu des points de contact entre une droite issue d'un point fixe F avec un cercle roulant sur une droite fixe passant par F.

Une droite variable (D') passant par O coupe la parallèle (D1) à (D0) passant par F en Q ; la strophoïde droite est le lieu du point M où le cercle centré en F passant par Q recoupe (D').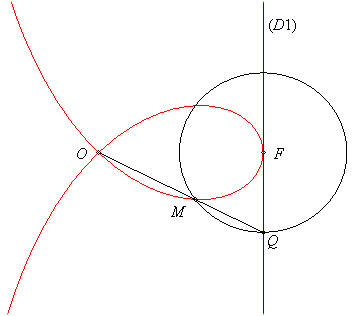
Étant donné un point  d'un cercle de centre O passant par A, la strophoïde droite est le lieu du point d'intersection M de la droite  avec la perpendiculaire en O à  (construction de Pierre Apel). La transformation  est involutive par construction. Définie analytiquement par , c'est une transformation quadratique à l'instar de la transformation de Newton.
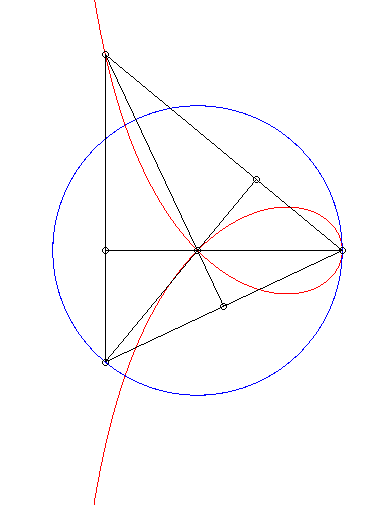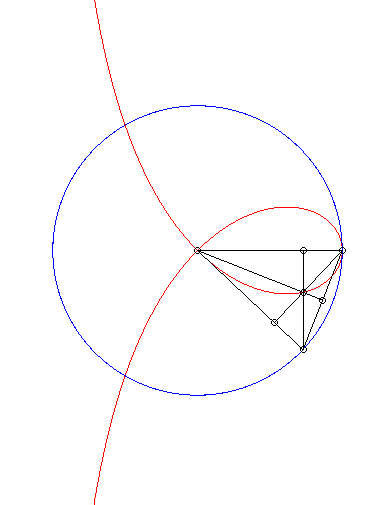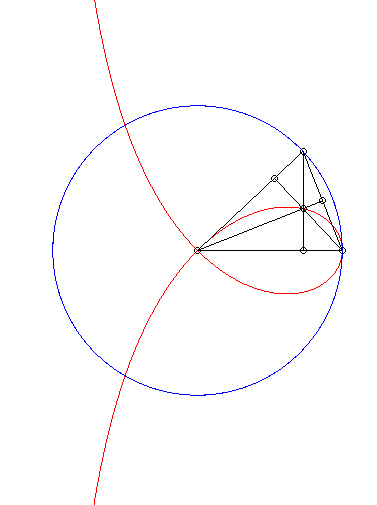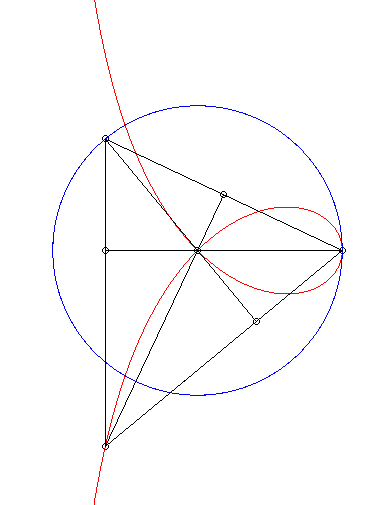
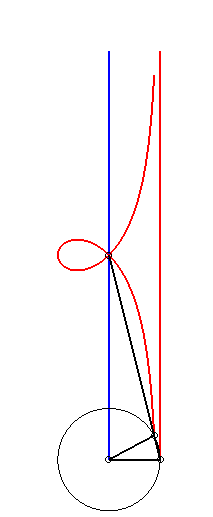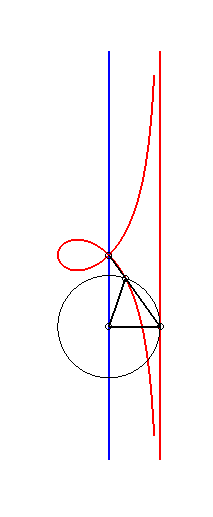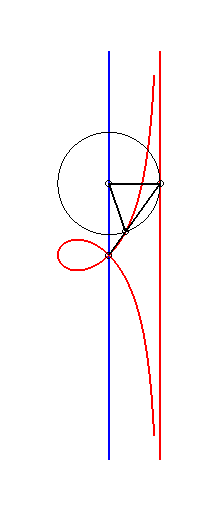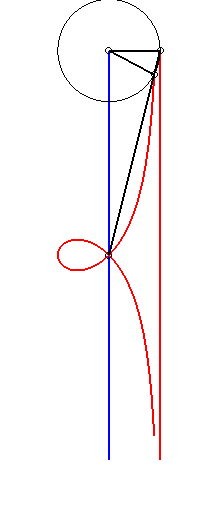
La strophoïde droite est le lieu de l'orthocentre d'un triangle dont deux sommets A et B sont fixes et le troisième décrit un cercle de rayon [AB]. Cf. une construction similaire du bicorne.
Si (C) est le cercle de centre O passant par F et G le point diamétralement opposé à F, la strophoïde droite est le lieu des points M tels que si P est l'un des points d'intersection de la perpendiculaire à (OF) passant par M avec (C), les droites (OM) et (GP) sont parallèles (construction de Rosillo).

 
 

La strophoïde droite possède aussi l'élégante construction en 3D suivante : si  (C) est le cylindre de révolution d'axe (D0) et passant par F, la strophoïde droite est le lieu des foyers des ellipses sections du cône (C) avec les plans perpendiculaires au plan de la strophoïde et passant par F. Ceci montre que la droite (D0) est la médiane de pôle F de la strophoïde avec elle-même.

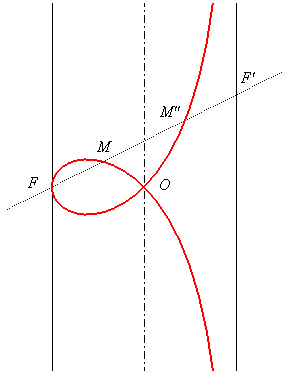
L'ellipse de sommets F et F' a pour foyers M et M".

 
 

L'équation polaire  montre que la strophoïde est la cissoïdale du kappa et de son asymptote.

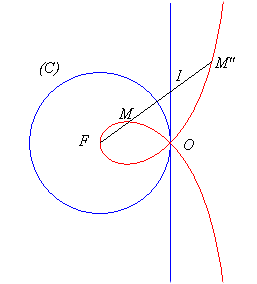
L'équation complexe ci-dessus montre que pour un droite passant par F, les deux points d'intersection avec la strophoïde sont inverses l'un de l'autre dans l'inversion de cercle d'inversion le cercle (C) de centre F passant par O :

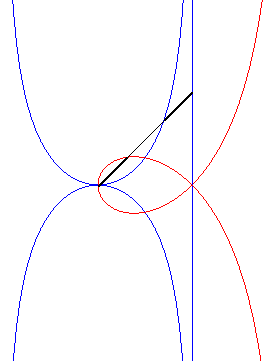
Comme toute cubique circulaire rationnelle, la strophoïde droite peut être définie comme :

    - la cissoïdale relativement à O d’un cercle de rayon a passant par O et d’une droite parallèle à la tangente en O et  située à une distance a du cercle (l'asymptote de la strophoïde) ;ici le cercle est le cercle (C) passant par O de centre F :
 

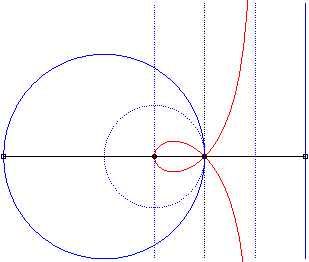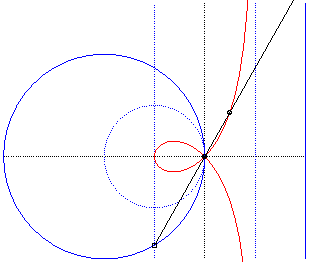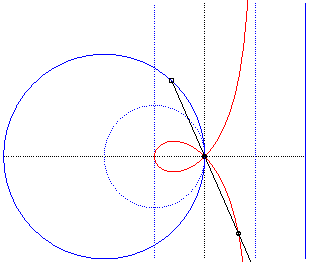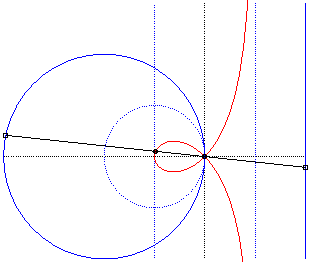La strophoïde est la cissoïdale du cercle pointillé et de la droite pointillée externe, donc aussi la médiane du cercle et de la droite pleins, homothétiques des précédents.

    - la podaire d’une parabole par rapport au pied de sa directrice (ici de la parabole de sommet F et de directrice l'axe de la strophoïde (d'équation ), par rapport au pied O de cet axe).

La strophoïde droite est donc l'enveloppe des cercles de diamètre joignant O et un point de la parabole ; autrement dit c'est une cyclique de déférente une parabole, avec une puissance d'inversion nulle et un pôle au pied de la directrice de la parabole.

    - l’inverse d’une hyperbole équilatère par rapport à l’un de ses sommets (ici de l'hyperbole équilatère de sommets O et F (d'équation : ), par rapport à O).

- par la méthode de l'équerre de Newton :	- comme kiéroïde

La strophoïde droite est aussi :
    - un cas particulier de nœud (cf. la deuxième équation polaire).
    - un cas particulier d'hyperbole cubique (cf. l'équation cartésienne)

- un cas particulier de sectrice de Maclaurin, d'où la construction à partir de 2 droites en rotation uniforme, l'une ayant la vitesse double de l'autre. Application : le lieu du centre du cercle inscrit dans le triangle ABC quand C décrit le cercle de centre A et de rayon AB est une strophoïde droite.

    - la projection stéréographique d’une fenêtre de Viviani.

Elle possède enfin une définition mécanique comme courbe du danseur de corde :

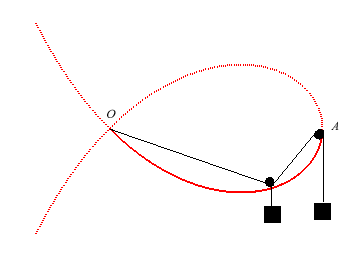Un funambule marche sur une corde attachée à un point fixe O à l'une de ses extrémités, passant par une poulie A située à même hauteur que l'extrémité attachée, et tendue par un contre-poids attaché à l'autre extrémité, le poids du funambule étant égal à celui du contre-poids.

© Robert FERRÉOL 2024