Notion étudiée par Leibniz en 1694 et Taylor en 1715.

 

Si  est définie par l'équation cartésienne (1) : f(x, y, t) = 0, l'équation de l'enveloppe s'obtient en éliminant t entre (1) et l'équation (2) : (équivalent au contour apparent suivant Oz de la surface f(x,y,z) = 0). Si  est définie paramétriquement par (M(u,t))u, la valeur en fonction de t du paramètre u du point caractéristique s'obtient en résolvant .

L'enveloppe d'une famille de courbes à un paramètre  est la famille  des points caractéristiques des courbes , points limites quand t' tend vers t des points d'intersection de  avec  ; la courbe  est tangente en chacun de ses points à une courbe  et "en général", toute courbe  est tangente en au moins un point à  ; les cas restrictifs sont les suivants :
    - sur un intervalle, les courbes  passent par un ou plusieurs points fixes, auquel cas, ce point appartient à l’enveloppe.
    - les courbes n'ont pas d'intersection entre elles (par exemple des cercles concentriques, ou des courbes dont les points d'intersection sont imaginaires).

Avec les notations ci-dessus dans le cas paramétrique, la condition étant symétrique en u et t, l'enveloppe des courbes  lieux des points (M(u,t))_t est la même que celle des courbes  ; l'enveloppe est en fait le lieu des points où une courbe de la première famille est tangente à une courbe de la deuxième. Les deux configurations sont dites duales l'une de l'autre.
 

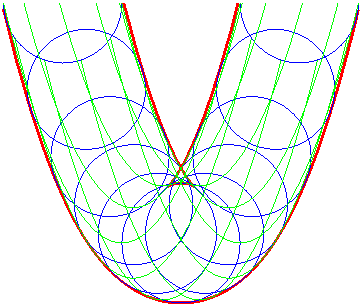Exemple : l'enveloppe d'un cercle  de rayon constant dont le centre décrit une parabole est une courbe parallèle à la parabole.  On a pris M(t, u) = (t + cos u, t² + sin u)

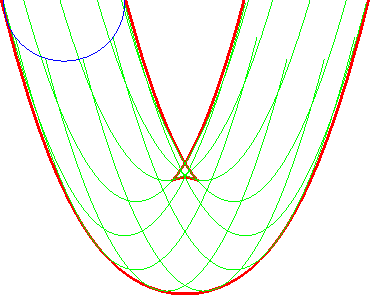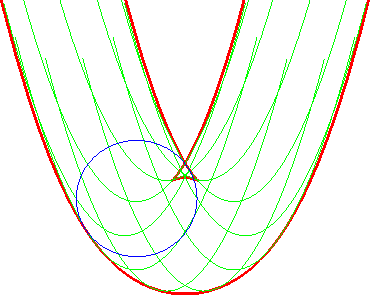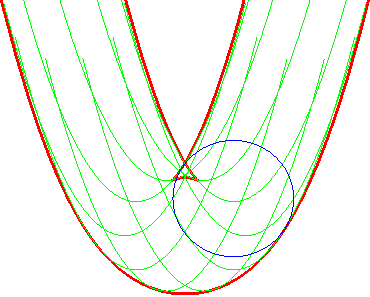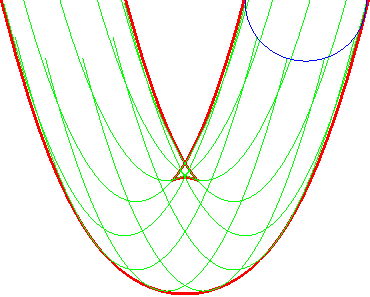
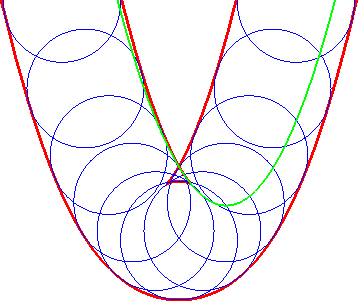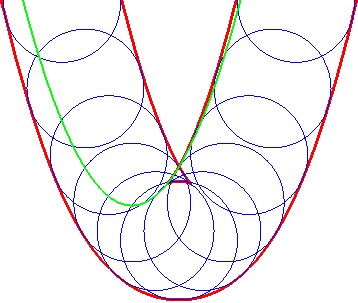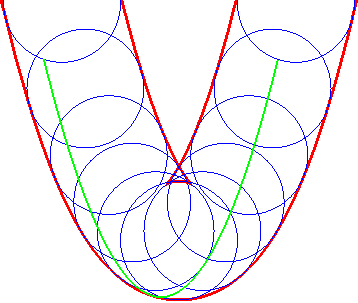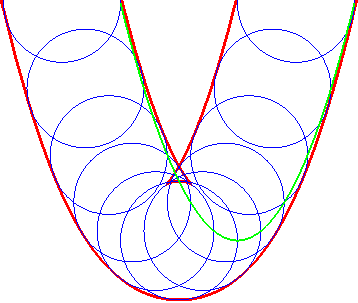
L'enveloppe des cercles  ...	... est aussi celle des paraboles (G'u)
Voir aussi un bel exemple de dualité à développante de cercle.

 

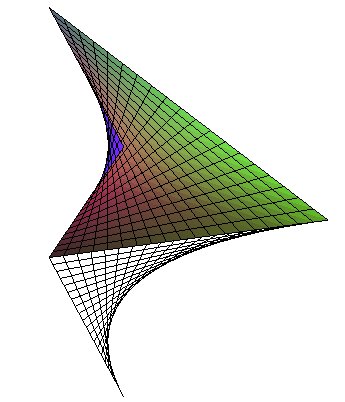
L'enveloppe de la famille de courbes f(x, y, t) = 0 est, comme indiqué ci-dessus, le contour apparent suivant Oz de la surface f(x, y, z) = 0 projeté sur le plan xOy. De même, l'enveloppe de la famille des courbes (M(u,t))u est le contour apparent suivant Oz de la surface paramétrée ((M(u,v),v))u,v  . Ici, par exemple, la parabole enveloppe des droites (((1–u)t,(1–t)u))u (joignant (t,0) et (0,1–t)), est le contour apparent de la surface (paraboloïde hyperbolique) (((1–u)v,(1–v)u,v))u,v .

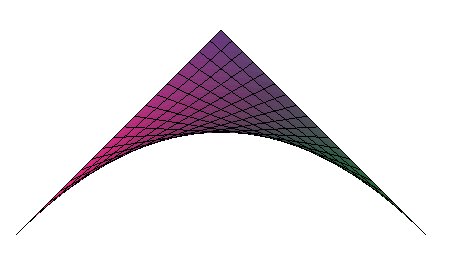L'enveloppe peut aussi être vue comme la solution singulière de l'équation différentielle dont les courbes  sont solutions.

Cas particulier : l'enveloppe d'une famille de droites est une courbe dont cette famille est la famille des tangentes.

On réalise physiquement les enveloppes de droites à l'aide de tableaux de fils.

 Exemples :
 - Toute courbe est l'enveloppe de ses tangentes, ou de ses cercles osculateurs.
 - La développée d'une courbe est l'enveloppe des normales à la courbe.
 - Les caustiques sont les enveloppes des rayons réfléchis par un système optique.
 - Les courbes parallèles à une courbe sont les enveloppes de cercles de rayon constant centrés sur cette courbe.
 - La podaire d'une courbe  par rapport à un point O est l'enveloppe des cercles de diamètre [OM] où M décrit , et la courbe orthotomique est l'enveloppe des cercles de centre M passant par O.
 - La polaire d'une courbe  par rapport à un cercle (C) est l'enveloppe des (droites) polaires par rapport à (C) des points de .
 - Une courbe anallagmatique est l'enveloppe des cercles orthogonaux au cercle d'inversion et centrés sur la déférente.
 - L'anticaustique d'une courbe est l'enveloppe d'un cercle centré sur la courbe et dont le rayon est dans un rapport constant avec la distance entre le centre du cercle et un point fixe.
 

- L'enveloppe d'une droite (AB) lorsque A et B se déplacent sur les axes Ox et Oy est         - une astroïde :  quand la longueur AB est constante égale à a, ou ce qui est équivalent, quand la distance du milieu de [AB] à O est constante égale à a/2,         - la réunion de quatre arcs de parabole :  quand OA + OB est constant égal à a (voir à courbe de Lamé),         - la réunion de quatre arcs de cercle de rayon a :quand le périmètre du triangle OAB reste constant égal à 2a,         - la réunion de deux hyperboles équilatères :  quand l'aire du triangle OAB est constante égale à .

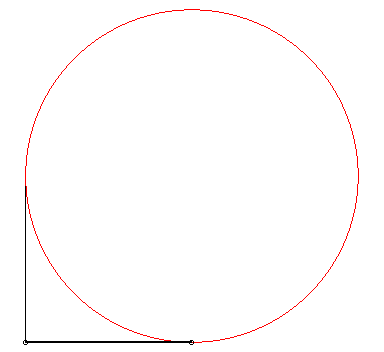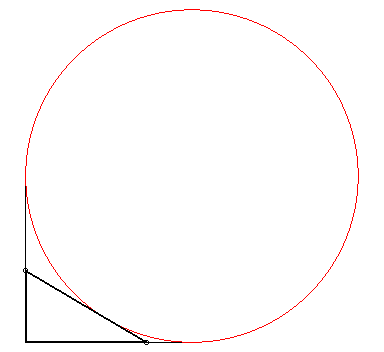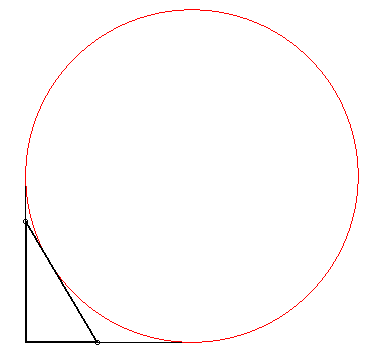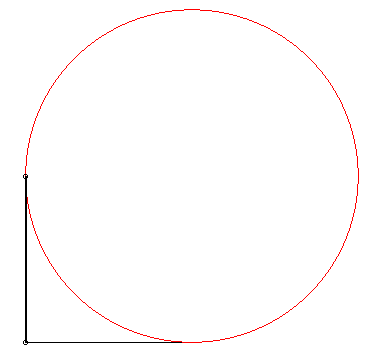
Le périmètre du triangle reste constant.

 - lorsque deux points A et B se déplacent sur un cercle avec des vitesses proportionnelles, la droite (AB) enveloppe des épi- et hypocycloïdes) (voir à génération de Cremona).

- Dans un mouvement plan sur plan, il est souvent intéressant de considérer l'enveloppe dans le plan fixe d'une droite du plan mobile .

 - La parabole de tir est l'enveloppe de toutes les trajectoires des tirs issus d'un point donné avec une vitesse de départ constante.

Voir aussi les enveloppes de surfaces et les enveloppes de courbes 3d.
 

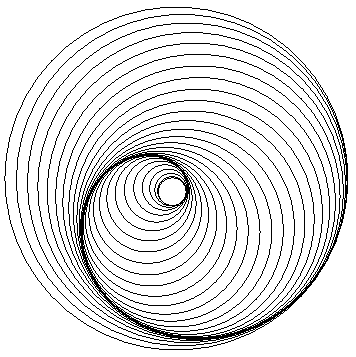
Ensemble de cercles osculateurs à une spirale d'Archimède. Il n'est même pas besoin de tracer l'enveloppe...

 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2023