Développante de cercle

DÉVELOPPANTE DE CERCLE
Circle involute, Kreisevolvente

Autre nom : anti-clothoïde.

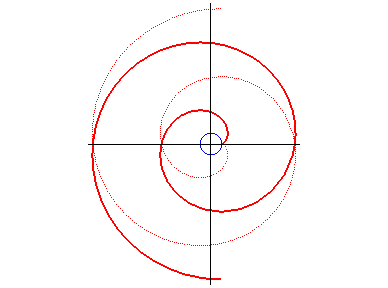
	Paramétrisation cartésienne : (développante du cercle de centre O et de rayon a, avec contact en (a, 0)). Paramétrisation complexe : . Paramétrisation polaire : (avec ). Équation polaire : , . Angle tangentiel cartésien : . Abscisse curviligne : . Rayon de courbure : . Équation intrinsèque 1 : . Équation intrinsèque 2 : . Équation podaire : . Equation différentielle cartésienne : .
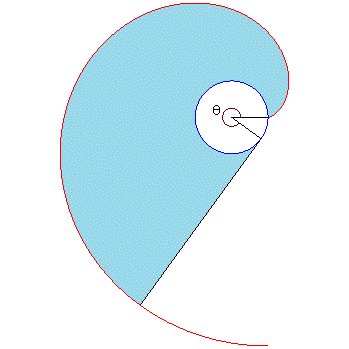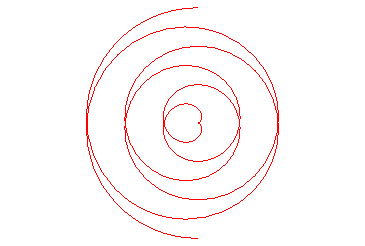
	Aire balayée par la tangente pour t allant de 0 à : (valable pour , sauf à compter les feuillets).

La définition de cette courbe tient dans son nom (voir à développante) !

La développante de cercle est donc la courbe dont les normales restent tangentes à un cercle fixe.
Plus concrètement, c’est la courbe que trace une main déroulant une bobine de fil tenue dans l'autre main.

Inversement, si l'on fait tourner une développante de cercle autour du centre du cercle générateur, chaque tangente au cercle reste constamment normale à la développante.

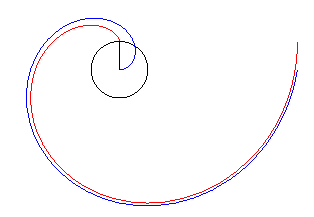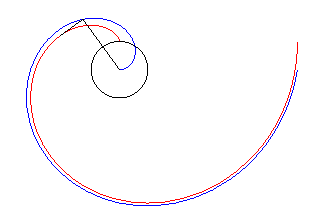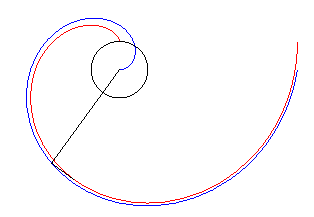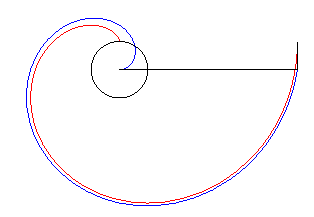
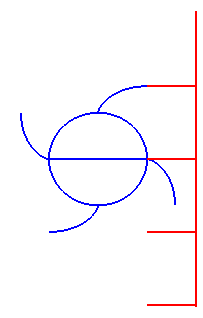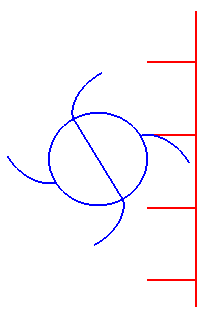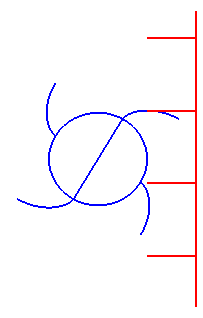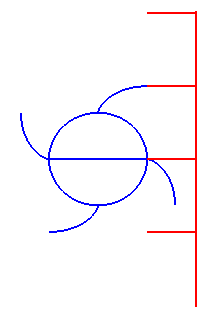
Pour t grand, la développante de cercle est asymptote à la spirale d'Archimède d'équation qui est d'ailleurs aussi sa podaire par rapport à O.

Cette dernière propriété a pour conséquence la suivante : si l'on fait tourner une développante de cercle uniformément autour de son centre, les tangentes à la développante ayant une direction donnée se déplacent en un mouvement de translation uniforme : c'est la raison pour laquelle les cames ont des profils de développante de cercle :

La développante de cercle possède aussi une définition cinématique, due aux relations : : c’est la courbe qui, parcourue d’un mouvement uniformément varié, est telle que la vitesse de rotation de la tangente est constante (d'où son nom d'anti-clothoïde : car la clothoïde, elle, est la courbe qui, parcourue d’un mouvement uniforme, est telle que la vitesse de rotation de la tangente est linéaire).

Autre définition cinématique :
Une personne P marche sur un plateau tournant à vitesse constante autour d'un point O ; le mouvement de P sur le plateau est rectiligne uniforme de vitesse v et ne passe pas par O. Si v = k w /a où a est la distance de la droite de parcours à O, la trajectoire de P est donnée par ; c'est donc une développante de cercle lorsque k = 1.
Inversement, la trace d'une bille roulant librement sur le plateau (ayant donc un mouvement rectiligne uniforme dans le repère fixe) est une telle courbe.

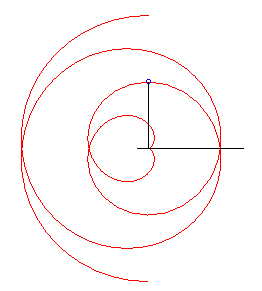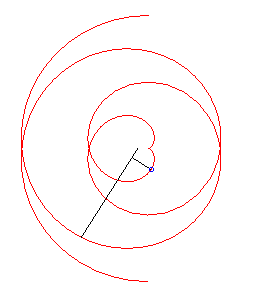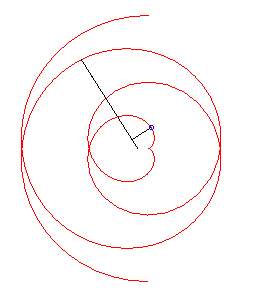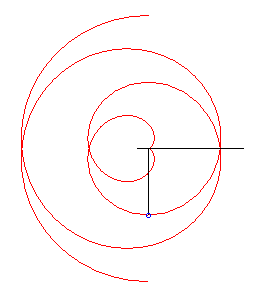
Cas k = 1 : développante de cercle. Cas k = -1.

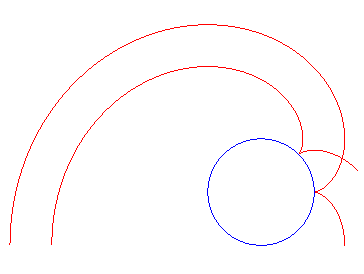
Comme toute famille de développantes d'une même courbe, les développantes d'un même cercle sont parallèles entre elles (la développante de cercle est d'ailleurs la seule courbe isométrique à ses parallèles).
Plus précisément l'image par une rotation d'angle de la développante donne une parallèle à une distance .

Si l'on prend en particulier , on retombe sur la même courbe ; la développante de cercle est donc une courbe autoparallèle ; ses spires sont distantes de .
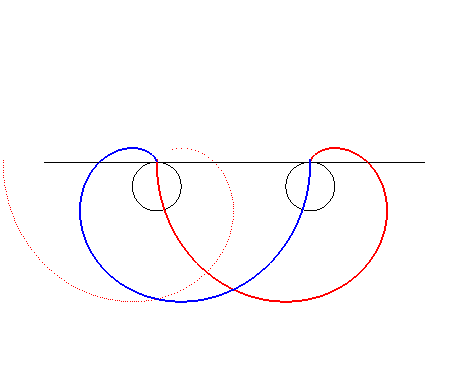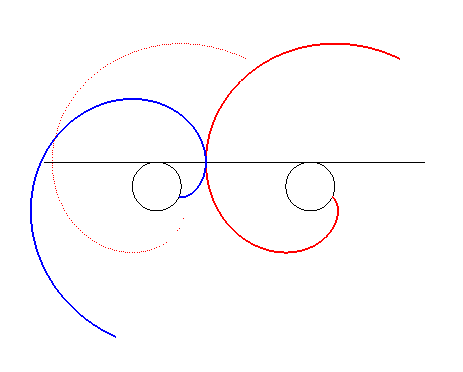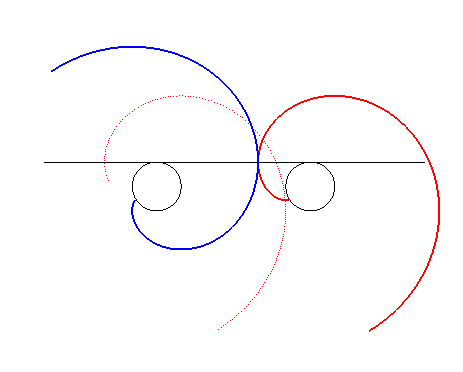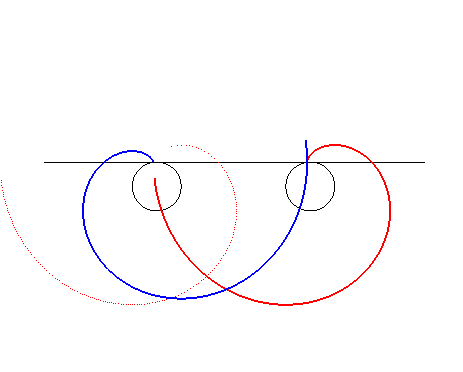Ceci a pour conséquence que si on translate une développante de cercle de perpendiculairement à son axe de symétrie, que l'on trace la droite joignant les deux rebroussements, et que l'on fait tourner à même vitesse les deux développantes autour de leurs centres, les deux développantes restent constamment en contact, et ceci perpendiculairement à cette droite.

Ceci a été appliqué à la fabrication d'engrenages (formés ici chacun de trois portions de développantes de cercles) dits engrenages paradoxaux, car tournant dans le même sens.
Bien suivre les points de contact sur les lignes noires.

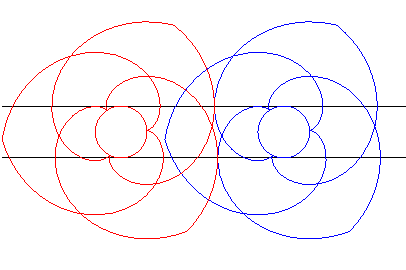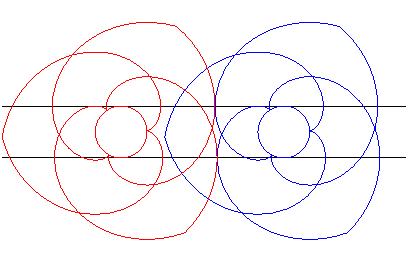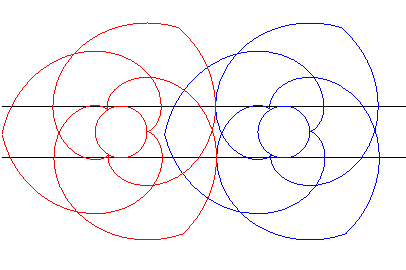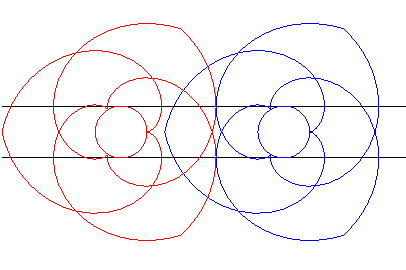
Animation réalisée par J. Lefort

Faisons maintenant subir à la développante translatée une symétrie par rapport à la normale commune ; les deux développantes restent toujours en contact, mais tournent cette fois en sens contraire.
Remarque : Le contact se fait avec glissement (le point de contact n'est pas sur la droite joignant les deux centres de rotation) mais suffisamment léger pour ne pas poser de problèmes d'échauffement en pratique. Ce ne sont donc pas deux profils conjugués.

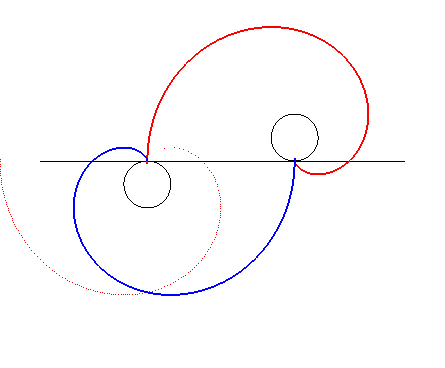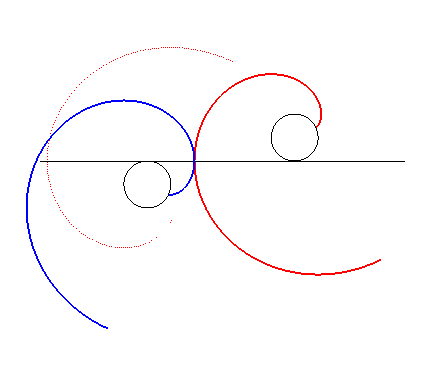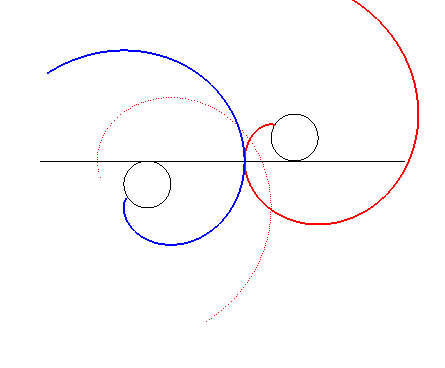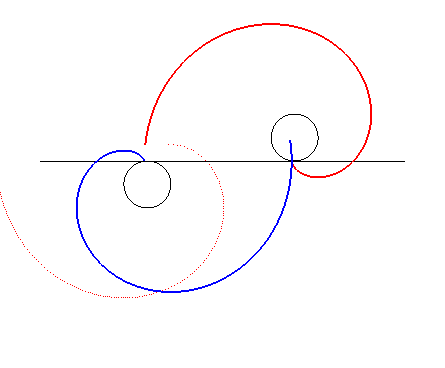Les mêmes engrenages que ci-dessus placés cette fois de part et d'autre de la droite tournent donc en sens inverse l'un de l'autre.
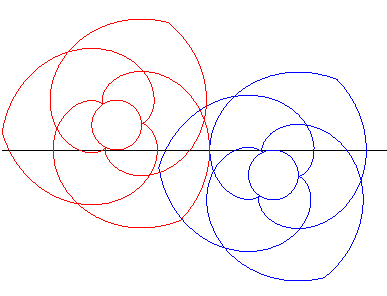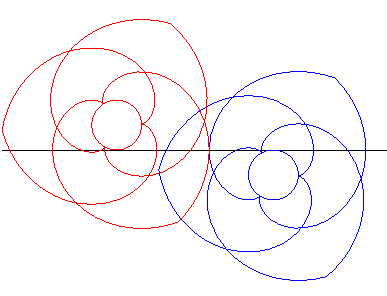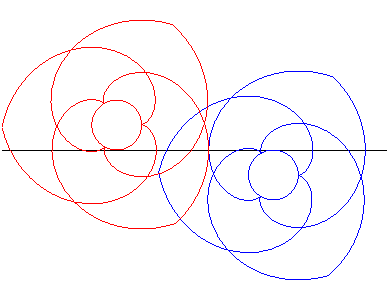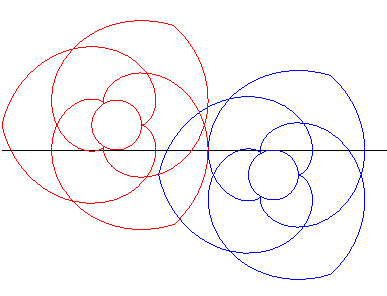
Animation réalisée par J. Lefort

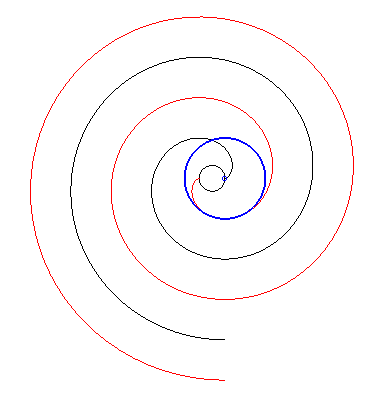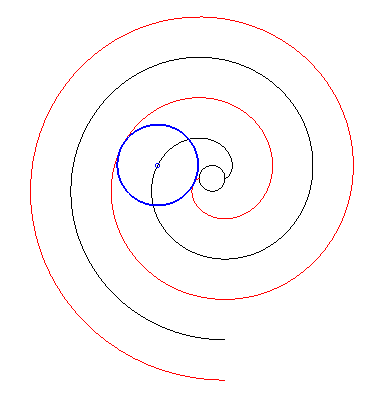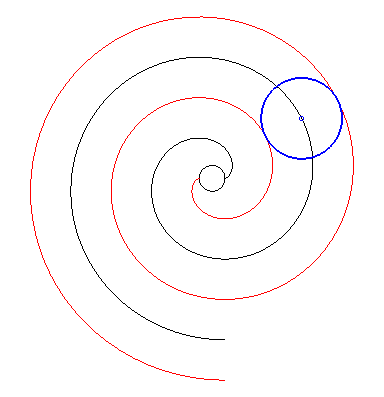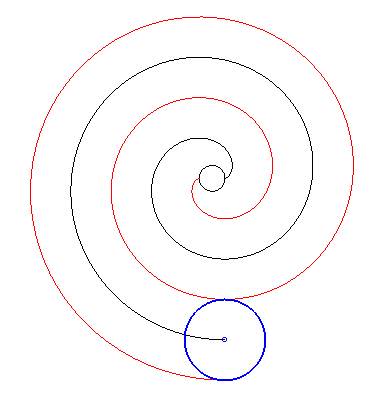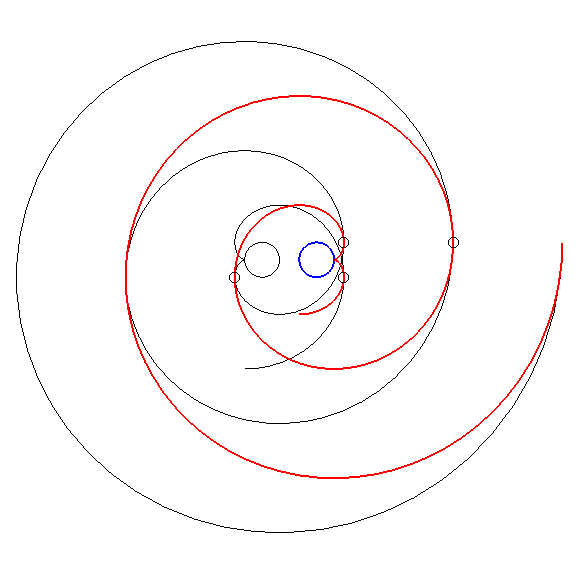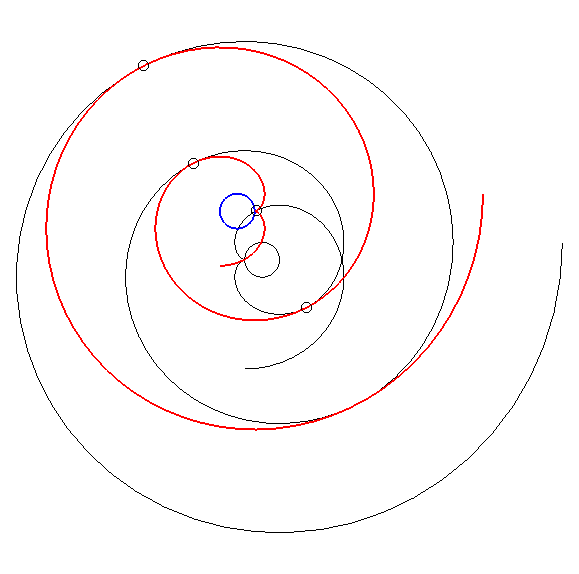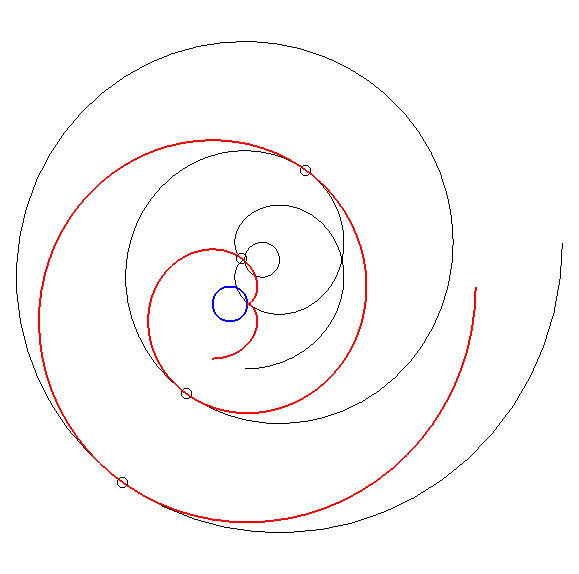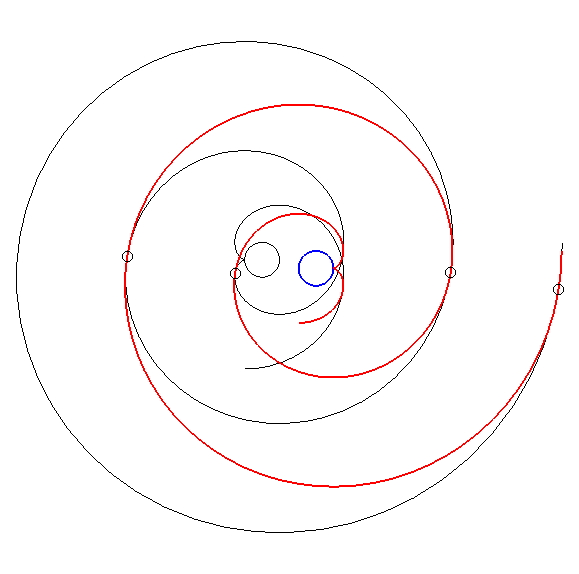
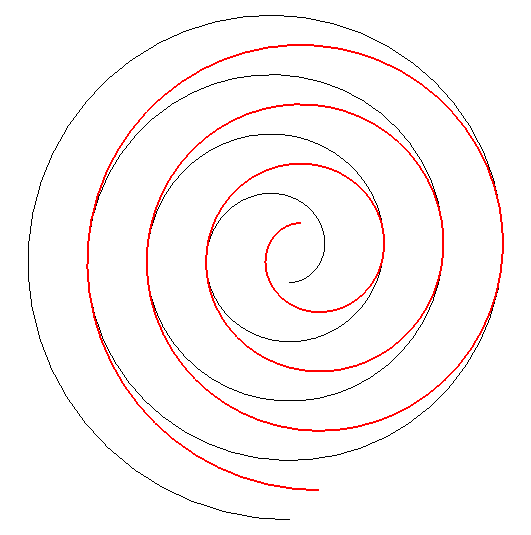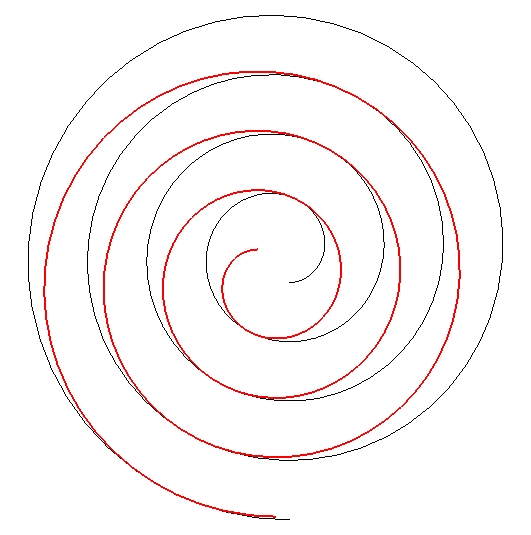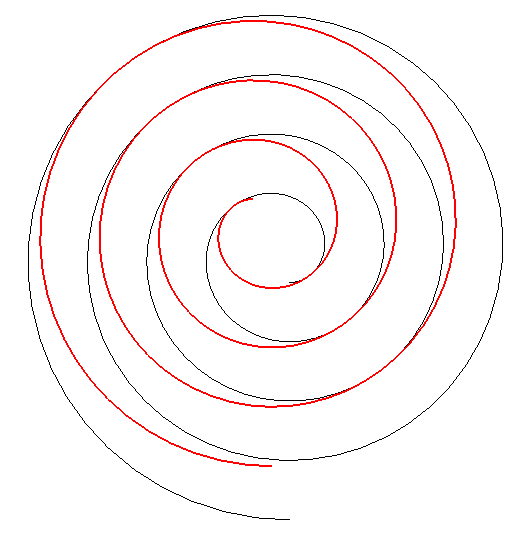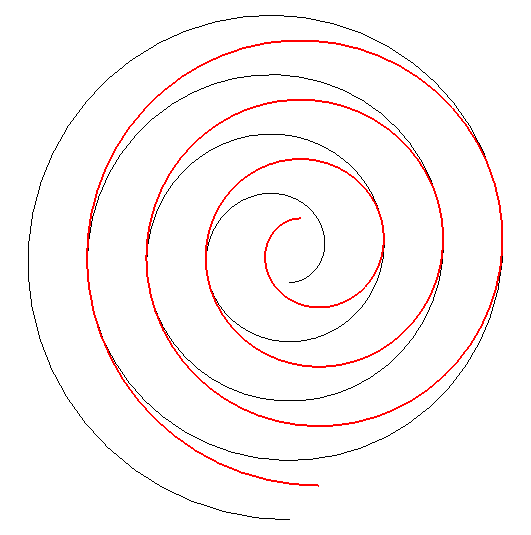
Autre cas particulier de courbe parallèle : la développante symétrique par rapport au centre du cercle est parallèle à la courbe de départ avec une distance (c'est en quelque sorte la courbe centrale de la développante de départ) : un cercle de rayon centré sur une développante de cercle enveloppe donc la développante symétrique.

Par dualité à partir de la propriété précédente, on obtient alors la propriété suivante : considérons une développante de cercle de rayon a et de centre O ; si l'on fait effectuer à cette développante (en rouge ci-dessous) un mouvement de translation de sorte que son centre décrive un cercle de centre O et de rayon , alors l'enveloppe de la famille de courbes obtenue est la développante de cercle symétrique par rapport à O de la première. Et il y a une infinité de points de tangence (2 par spire).
Conseil : suivre des yeux un point de tangence. Cette propriété découverte par Léon Creux (cf. brevet en 1905 et article en 1911) est utilisée dans la fabrication des compresseurs de gaz dits compresseurs à spirale, ou compresseurs scroll.
La famille des spirales mobiles est définie par et les points caractéristiques sont donnés par .

Animation montrant l'utilisation de développantes de cercle dans des engrenages classiques. Les développantes restent en contact sur une tangente commune aux deux cercles.

La section de l'hélicoïde développable par un plan perpendiculaire à l'axe est une développante de cercle.

La projection d'une hélice du paraboloïde de révolution est une développante de cercle.

La développante de cercle est une sectrice et une quadratrice.

Son inverse par rapport à son centre est la spirale tractrice, et son antipodaire est la caustique inverse de cercle.

Ses développantes sont les courbes dont le rayon de courbure est égal à la distance à O, plus une constante, l'une d'entre elles étant la spirale de Norwich.

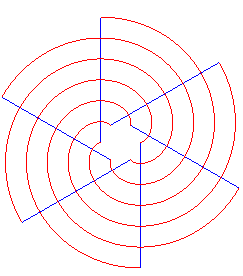
Les demi-développantes d'un cercle donné forment un système double orthogonal avec les demi-tangentes au cercle

Engrenages en développantes de cercles réalisés par Vincent Viton.

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres

La développante de cercle est donc la courbe dont les normales restent tangentes à un cercle fixe. Plus concrètement, c’est la courbe que trace une main déroulant une bobine de fil tenue dans l'autre main.
Inversement, si l'on fait tourner une développante de cercle autour du centre du cercle générateur, chaque tangente au cercle reste constamment normale à la développante.

Pour t grand, la développante de cercle est asymptote à la spirale d'Archimède d'équation qui est d'ailleurs aussi sa podaire par rapport à O.
Cette dernière propriété a pour conséquence la suivante : si l'on fait tourner une développante de cercle uniformément autour de son centre, les tangentes à la développante ayant une direction donnée se déplacent en un mouvement de translation uniforme : c'est la raison pour laquelle les cames ont des profils de développante de cercle :

Comme toute famille de développantes d'une même courbe, les développantes d'un même cercle sont parallèles entre elles (la développante de cercle est d'ailleurs la seule courbe isométrique à ses parallèles). Plus précisément l'image par une rotation d'angle de la développante donne une parallèle à une distance .
Si l'on prend en particulier , on retombe sur la même courbe ; la développante de cercle est donc une courbe autoparallèle ; ses spires sont distantes de . Ceci a pour conséquence que si on translate une développante de cercle de perpendiculairement à son axe de symétrie, que l'on trace la droite joignant les deux rebroussements, et que l'on fait tourner à même vitesse les deux développantes autour de leurs centres, les deux développantes restent constamment en contact, et ceci perpendiculairement à cette droite.
Ceci a été appliqué à la fabrication d'engrenages (formés ici chacun de trois portions de développantes de cercles) dits engrenages paradoxaux, car tournant dans le même sens. Bien suivre les points de contact sur les lignes noires.	Animation réalisée par J. Lefort
Faisons maintenant subir à la développante translatée une symétrie par rapport à la normale commune ; les deux développantes restent toujours en contact, mais tournent cette fois en sens contraire. Remarque : Le contact se fait avec glissement (le point de contact n'est pas sur la droite joignant les deux centres de rotation) mais suffisamment léger pour ne pas poser de problèmes d'échauffement en pratique. Ce ne sont donc pas deux profils conjugués.
Les mêmes engrenages que ci-dessus placés cette fois de part et d'autre de la droite tournent donc en sens inverse l'un de l'autre.	Animation réalisée par J. Lefort
Autre cas particulier de courbe parallèle : la développante symétrique par rapport au centre du cercle est parallèle à la courbe de départ avec une distance (c'est en quelque sorte la courbe centrale de la développante de départ) : un cercle de rayon centré sur une développante de cercle enveloppe donc la développante symétrique.