Paramétrisation cartésienne :  (où a est le rayon du cercle de base de l'hélice et 2pb son pas). . Lignes de courbures : les génératrices et les courbes de niveau.

L'hélicoïde développable est la surface engendrée par les tangentes à une hélice circulaire.
 

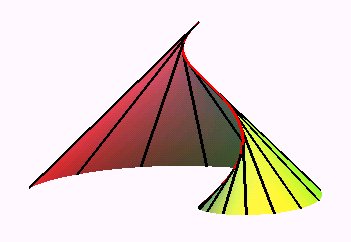
Figure montrant l'hélice et ses demi-tangentes.

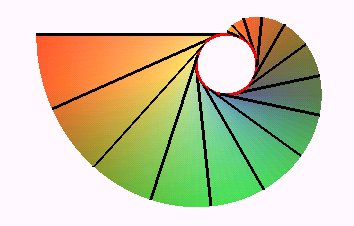
Vue de dessous

C'est une surface d'égale pente (comme toute surface engendrée par les tangentes à une hélice), et c'est le seul hélicoïde qui soit développable.
Étant engendrée par une droite d'un plan roulant sans glisser sur un cylindre de révolution, c'est une surface moulure.
 

Les courbes de niveau (sections par des plans horizontaux) sont des développantes de cercles ; ce sont les développantes de l'hélice arête de rebroussement et aussi des développantes du cylindre contenant l'hélice.

 

La section par le plan y = 0 a pour paramétrisation :  ; l'hélicoïde développable résulte donc du mouvement hélicoïdal de cette courbe le long de son axe :

 

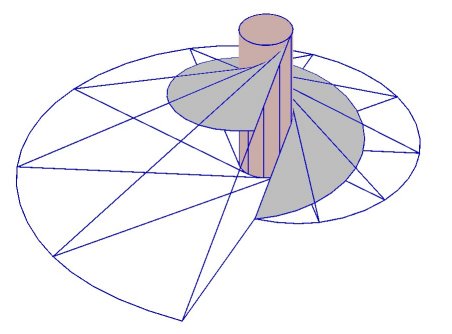
Modélisation de l'hélicoïde développable réalisée par Robert March, professeur à l'école d'architecture de Paris, qui propose aussi la réalisation concrète suivante : prendre un rouleau de papier alu, dérouler une longueur d'alu égale à la largeur, former un triangle rectangle en pliant en diagonale, ré-enrouler, et re-dérouler en gardant la feuille d'alu tendue ; la diagonale engendre l'hélicoïde développable et sa pointe une belle développante de cercle.

Escalier d'entrée du Louvre par la Pyramide. Bien sûr les marches génèrent un hélicoïde droit mais la surface sous l'escalier (l'intrados) semble être au moins de manière approchée une portion d'hélicoïde développable : en témoigne le fait que le contour apparent de la surface est formé de génératrices quasi rectilignes (cf. les traits rouges).

 

surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2019